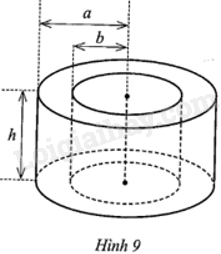
Giải bài 11 trang 126 sách bài tập toán 9 - Cánh diều tập 2Các kích thước của hai hình trụ (T) và (T’) (hình trụ (T) ở bên ngoài và hình trụ (T’) ở bên trong) được cho ở Hình 9. a) Viết biểu thức tính thể tích phần ở giữa hai hình trụ (T) và (T’) theo a, b và h. b) Tính chiều cao h, biết a = 16 cm, (b = frac{3}{4}a) và thể tích phần ở giữa hai hình trụ (T) và (T’) là 224π cm3. Quảng cáo
Đề bài Các kích thước của hai hình trụ (T) và (T’) (hình trụ (T) ở bên ngoài và hình trụ (T’) ở bên trong) được cho ở Hình 9.
a) Viết biểu thức tính thể tích phần ở giữa hai hình trụ (T) và (T’) theo a, b và h. b) Tính chiều cao h, biết a = 16 cm, \(b = \frac{3}{4}a\) và thể tích phần ở giữa hai hình trụ (T) và (T’) là 224π cm3. Phương pháp giải - Xem chi tiết Dựa vào: Thể tích hình trụ: \(V = \pi {r^2}h\). Lời giải chi tiết a) Thể tích của hình trụ (T) là: πa2h (cm3). Thể tích của hình trụ (T’) là: πb2h (cm3). Thể tích phần ở giữa hai hình trụ (T) và (T’) theo a, b và h là: πa2h – πb2h = πh(a2 – b2) (cm3). b) Ta có a = 16 (cm), \(b = \frac{3}{4}a = \frac{3}{4}.16 = 12\) (cm). Khi đó, thể tích phần ở giữa hai hình trụ (T) và (T') là: πh.(162 – 122) = 112πh (cm3). Theo bài, thể tích phần ở giữa hai hình trụ (T) và (T’) là 224π cm3 nên ta có: 112πh = 224π, suy ra h = 2 (cm). Vậy h = 2 cm.
|




















Danh sách bình luận