Giải bài 8 trang 124, 125 vở thực hành Toán 9Cho tam giác ABC ((widehat A) vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A’. Chứng minh rằng: a) BA và BA’ là hai tiếp tuyến cắt nhau của đường tròn (C; CA); b) CA và CA’ là hai tiếp tuyến cắt nhau của đường tròn (B; BA). Quảng cáo
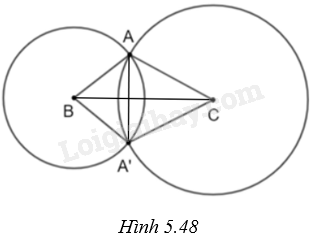
Đề bài Cho tam giác ABC (\(\widehat A\) vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A’. Chứng minh rằng: a) BA và BA’ là hai tiếp tuyến cắt nhau của đường tròn (C; CA); b) CA và CA’ là hai tiếp tuyến cắt nhau của đường tròn (B; BA). Phương pháp giải - Xem chi tiết a) + Chứng minh \(AB \bot AC\), \(AB \bot AC\), mà \(A \in \left( {C;CA} \right)\) nên BA là tiếp tuyến của đường tròn (C; CA) + Chứng minh \(\Delta ABC = \Delta A'BC\left( {c.c.c} \right)\) nên \(\widehat {BAC} = \widehat {BA'C} = {90^o}\), do đó \(A'B \bot A'C\), suy ra BA’ là tiếp tuyến của đường tròn (C; CA). b) + \(AB \bot AC\) và \(A \in \left( {B;BA} \right)\) nên CA là tiếp tuyến của đường tròn (B; BA). Lời giải chi tiết (H.5.48)
a) Tam giác ABC vuông tại A nên \(AB \bot AC\), mà \(A \in \left( {C;CA} \right)\) do đó BA là tiếp tuyến của đường tròn (C; CA). Hai tam giác ABC và A’BC có: BC là cạnh chung, \(AB = A'B\) (cùng bằng bán kính của (B; AB)), \(AC = A'C\) (cùng bằng bán kính của (C; AC)) Do đó, \(\Delta ABC = \Delta A'BC\left( {c.c.c} \right)\), suy ra \(\widehat {BAC} = \widehat {BA'C} = {90^o}\), hay \(A'B \bot A'C\). Mặt khác, \(A' \in \left( {C;CA'} \right)\) nên BA’ là tiếp tuyến của đường tròn (C; CA). Vậy BA và BA’ là hai tiếp tuyến cắt nhau của đường tròn (C; CA); b) Ta có: \(AB \bot AC\) và \(A \in \left( {B;BA} \right)\) nên CA là tiếp tuyến của đường tròn (B; BA). Tương tự, CA’ là tiếp tuyến của đường tròn (B; BA). Vậy CA và CA’ là hai tiếp tuyến cắt nhau của đường tròn (B; BA).
|




















Danh sách bình luận