Trang chủ
Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT

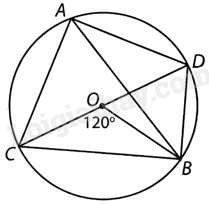
Giải bài 7 trang 89, 90 vở thực hành Toán 9 tập 2

Cho các điểm A, B, C, D trên đường tròn (O) như hình bên. Biết rằng CD là đường kính của (O) và (widehat {BOC} = {120^o}), hãy tính số đo các góc CAD và CDB.

Quảng cáo

Đề bài

Cho các điểm A, B, C, D trên đường tròn (O) như hình bên. Biết rằng CD là đường kính của (O) và \(\widehat {BOC} = {120^o}\), hãy tính số đo các góc CAD và CDB.

Phương pháp giải - Xem chi tiết

Xét trong đường tròn (O), ta có:

- Góc nội tiếp CDB và góc ở tâm BOC cùng chắn cung nhỏ BC nên \(\widehat {CDB} = \frac{1}{2}\widehat {BOC}\);

- Vì CD là đường kính nên góc nội tiếp CAD chắn nửa đường tròn (O) nên tính được góc CAD.

Lời giải chi tiết

Xét trong đường tròn (O), ta có:

- Góc nội tiếp CDB và góc ở tâm BOC cùng chắn cung nhỏ BC nên \(\widehat {CDB} = \frac{1}{2}\widehat {BOC} = {60^o}\);

- Vì CD là đường kính nên góc nội tiếp CAD chắn nửa đường tròn (O) và do đó: \(\widehat {CAD} = {90^o}\).

  • Giải bài 8 trang 90 vở thực hành Toán 9 tập 2

    Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC của tam giác ABC lần lượt tại F và E. a) Cho BE cắt CF tại H. Chứng minh rằng AH vuông góc với BC. b) Chứng minh rằng EF song song với BC.

  • Giải bài 6 trang 89 vở thực hành Toán 9 tập 2

    Trên sân bóng, khi quả bóng được đặt tại điểm phạt đền thì có góc sút bằng ({36^o}) và quả bóng cách mỗi cọc gôn 11,6m như hình dưới đây. Hỏi khi quả bóng đặt ở vị trí cách điểm phạt đền 11,6m thì góc sút bằng bao nhiêu?

  • Giải bài 5 trang 88, 89 vở thực hành Toán 9 tập 2

    Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A), N (khác B). Gọi P là giao điểm của BM và AN như hình bên. Chứng minh rằng SP vuông góc với AB.

  • Giải bài 4 trang 88 vở thực hành Toán 9 tập 2

    Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) như hình bên. a) Biết rằng (widehat {AOC} = {60^o},widehat {BOD} = {80^o}). Tính số đo của góc AID. b) Chứng minh rằng (IA.IB = IC.ID).

  • Giải bài 3 trang 88 vở thực hành Toán 9 tập 2

    Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X như hình bên. Tính số đo góc AXB biết rằng (widehat {ADB} = {30^o},widehat {DBC} = {50^o}).

Quảng cáo
Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
close