Giải bài 59 trang 125 sách bài tập toán 9 - Cánh diều tập 1Tam giác Reuleaux là hình tạo nên từ phần giao nhau của ba đường tròn cùng bán kính, tâm của mỗi đường tròn chính là giao điểm của hai đường tròn còn lại. Tạo tam giác Reuleaux từ ba đường tròn (A), (B), (C) (Hình 56). Tính số đo các cung nhỏ BaC, CbA, AcB của tam giác Reuleaux. Nêu nhận xét về số đo của các cung tròn đó. Quảng cáo
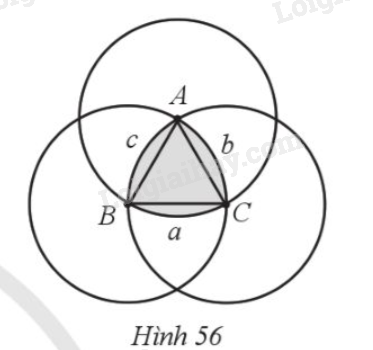
Đề bài Tam giác Reuleaux là hình tạo nên từ phần giao nhau của ba đường tròn cùng bán kính, tâm của mỗi đường tròn chính là giao điểm của hai đường tròn còn lại. Tạo tam giác Reuleaux từ ba đường tròn (A), (B), (C) (Hình 56). Tính số đo các cung nhỏ BaC, CbA, AcB của tam giác Reuleaux. Nêu nhận xét về số đo của các cung tròn đó.
Phương pháp giải - Xem chi tiết Bước 1: Chứng minh tam giác ABC đều, suy ra \(\widehat {ABC} = \widehat {BCA} = \widehat {CAB} = 60^\circ \). Bước 2: Tính số đo các cung CbA, AcB, BaC. Lời giải chi tiết Do 3 đường tròn có cùng bán kính nên \(AB = BC = CA\), suy ra tam giác ABC đều, do đó \(\widehat {ABC} = \widehat {BCA} = \widehat {CAB} = 60^\circ \). Ta lại có \(\widehat {ABC},\widehat {BCA},\widehat {CAB}\) lần lượt là các góc ở tâm của 3 đường tròn (B), (C), (A) nên số đo các cung CbA, AcB, BaC bằng 60⁰. Vậy số đo 3 cung tròn trên bằng nhau.
|




















Danh sách bình luận