Giải bài 5.33 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1

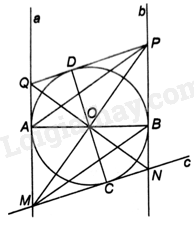
Đề bài

Cho đường tròn (O), đường thẳng a tiếp xúc với (O) tại A, đường thẳng b tiếp xúc với (O) tại B sao cho a//b. Gọi C là một điểm tùy ý thuộc (O), khác A và B. Tiếp tuyến c của (O) tại C cắt a và b lần lượt tại M và N.

a) Chứng minh AB là một đường kính của (O).

b) Gọi D, P và Q lần lượt là các điểm đối xứng với C, M và N qua tâm O. Chứng minh rằng \(D \in \left( O \right),P \in b\) và \(Q \in a\).

c) Chứng minh rằng PQ tiếp xúc với (O) tại D.

d) Chứng minh tứ giác MNPQ là một hình thoi.

Lời giải chi tiết

a) Vì a tiếp xúc với (O) tại A hay a là tiếp tuyến của (O) tại A. Do đó, \(a \bot OA\).

Vì b tiếp xúc với (O) tại B hay b là tiếp tuyến của (O) tại B. Do đó, \(b \bot OB\).

Lại có: a//b. Do đó, ba điểm O, A, B thẳng hàng.

Vì \(OA = OB\) nên AB là đường kính của (O).

b) Vì C thuộc (O) và D đối xứng với C qua O nên do tính đối xứng của đường tròn, suy ra D thuộc (O).

Tứ giác AMBP có: \(OA = OB\), \(OM = OP\) (P đối xứng với M qua O) nên tứ giác AMBP là hình bình hành, suy ra BP//AM. Vì M, A thuộc đường thẳng a nên BP//a.

Mà b//a nên đường thẳng \(BP \equiv b\). Khi đó, P thuộc b.

Chứng minh tương tự ta có Q thuộc a. 

c) Tam giác COM và tam giác DOP có: \(OM = OP,OC = OD\) (vì D đối xứng với C qua O), \(\widehat {MOC} = \widehat {POD}\) (hai góc đối đỉnh) nên \(\Delta COM = \Delta DOP\left( {c.g.c} \right)\), suy ra \(\widehat {PDO} = \widehat {MCO} = {90^o}\).

Tương tự ta có: \(\Delta CON = \Delta DOQ\left( {c.g.c} \right)\), suy ra \(\widehat {QDO} = \widehat {NCO} = {90^o}\).

Ta có: \(\widehat {PDO} + \widehat {QDO} = \widehat {QDP} = {180^o}\) nên ba điểm P, D, Q thẳng hàng và PQ là tiếp tuyến của (O) tại D.

d) Tứ giác MNPQ có hai đường chéo MP và NQ cắt nhau tại trung điểm O của mỗi đường nên MNPQ là hình bình hành.

Vì MA và MC là hai tiếp tuyến cắt nhau tại M của (O) nên OM là tia phân giác của góc AOC.

Do đó, \(\widehat {AOM} = \widehat {MOC} = \frac{1}{2}\widehat {AOC}\).

Vì NB và NC là hai tiếp tuyến cắt nhau tại N của (O) nên ON là tia phân giác của góc BOC.

Do đó, \(\widehat {BON} = \widehat {NOC} = \frac{1}{2}\widehat {BOC}\).

Ta có:

\(\widehat {MOC} + \widehat {NOC} = \frac{1}{2}\left( {\widehat {AOC} + \widehat {BOC}} \right) \\= \frac{1}{2}{.180^o} = {90^o}.\)

Suy ra \(\widehat {MON} = {90^0}\) nên MP\( \bot \) NQ tại O.

Hình bình hành MNPQ có đường chéo MP vuông góc với NQ tại O.

Do đó, MNPQ là hình thoi.