Giải bài 5.26 trang 68 sách bài tập toán 9 - Kết nối tri thức tập 1

Đề bài

Cho tam giác ABC.

a) Chứng minh rằng hai đường tròn (B; BA) và (C; CA) cắt nhau. Gọi A’ là giao điểm khác A của hai đường tròn đó.

b) Chứng minh rằng A và A’ đối xứng nhau qua BC.

c) Biết rằng \(AA' = 24cm,AB = 15cm\) và \(AC = 13cm\). Tính độ dài BC.

Lời giải chi tiết

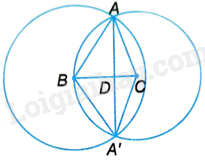
a) Áp dụng bất đẳng thức tam giác vào tam giác ABC ta có:

\(\left| {AB - AC} \right| < BC < AB + AC\) nên hai đường tròn (B; BA) và (C; CA) cắt nhau.

b) Tam giác ABC và tam giác A’B’C’ có: \(AC = A'C,AB = A'B\), BC chung nên \(\Delta ABC = \Delta A'B'C'\left( {c.c.c} \right)\).

Suy ra: \(\widehat {ABC} = \widehat {A'BC}\) .

Do đó, BC là phân giác của góc ABA’.

Vì \(AB = A'B\) nên tam giác AA’B cân tại B nên BC vừa là đường phân giác đồng thời là đường trung trực của tam giác AA’B.

Suy ra, BC là đường trung trực của AA’ nên A và A’ đối xứng nhau qua BC.

c) Gọi D là giao điểm của BC và AA’.

Theo b ta có: \(AD = DA'\) và \(BC \bot AA'\) tại D.

Do đó, tam giác ABD vuông tại D và tam giác ACD vuông tại D.

Vì \(AD = DA'\) nên \(AD = \frac{{AA'}}{2} = 12cm\).

Áp dụng định lí Pythagore vào tam giác ABD vuông tại D ta có:

\(B{D^2} + A{D^2} = A{B^2}\) nên \(BD = \sqrt {A{B^2} - A{D^2}}  = \sqrt {{{15}^2} - {{12}^2}}  = 9\left( {cm} \right)\)

Áp dụng định lí Pythagore vào tam giác ACD vuông tại D ta có:

\(C{D^2} + A{D^2} = A{C^2}\) nên \(CD = \sqrt {A{C^2} - A{D^2}}  = \sqrt {{{13}^2} - {{12}^2}}  = 5\left( {cm} \right)\)

Vậy \(BC = BD + DC = 9 + 5 = 14\left( {cm} \right)\).