Giải bài 5.23 trang 68 sách bài tập toán 9 - Kết nối tri thức tập 1

Đề bài

Vẽ hình và chứng minh phần b của Ví dụ 2.

Ví dụ 2: Cho đường tròn (O) và dây AB không là đường kính của (O).
a) Gọi O' là một điểm tùy ý nằm giữa O và A. Đường thẳng đi qua O' và song song với OB cắt AB tại C. Hãy xác định vị trí tương đối của (O) và (O'; O'C).
b) Vị trí tương đối của (O) và (O'; O'C) sẽ như thế nào nếu O' thẳng hàng với O và A, nhưng nằm ngoài đoạn OA?

Lời giải chi tiết

Trường hợp 1: O và O’ nằm cùng phía với A (O nằm giữa O’ và A).

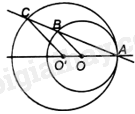
Vì CO’//OB nên $\Delta O'AC\backsim \Delta OAB$.

Vì OA=OB nên tam giác OAB cân tại O. Do đó, tam giác O’AC cân tại O’ và \(O'C = O'A\).

Lại có: \(OO' = O'A - OA = O'C - OA\). Do đó, đường tròn (O’; O’C) tiếp xúc trong với đường tròn (O; OA).

Trường hợp 2: O và O’ nằm khác phía với A (A nằm giữa O’ và O).

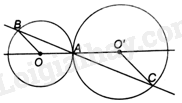
Vì CO’//OB nên $\Delta O'AC\backsim \Delta OAB$.

Vì OA=OB nên tam giác OAB cân tại O. Do đó, tam giác O’AC cân tại O’ và \(O'C = O'A\).

Lại có: \(OO' = O'A + OA = O'C + OA\). Do đó, đường tròn (O’; O’C) tiếp xúc ngoài với đường tròn (O; OA).