Giải bài 5 trang 9 SBT toán 10 - Chân trời sáng tạoXét dấu của các tam thức bậc hai sau: a) \(f\left( x \right) = {x^2} - 5x + 4\) b) \(f\left( x \right) = - \frac{1}{3}{x^2} + 2x - 3\) c) \(f\left( x \right) = 3{x^2} + 6x + 4\) Quảng cáo
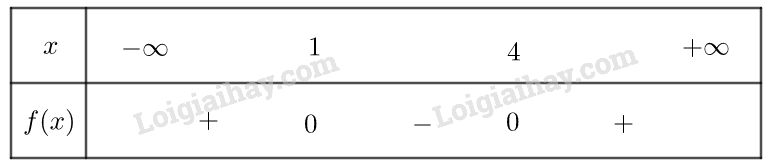
Đề bài Xét dấu của các tam thức bậc hai sau: a) \(f\left( x \right) = {x^2} - 5x + 4\) b) \(f\left( x \right) = - \frac{1}{3}{x^2} + 2x - 3\) c) \(f\left( x \right) = 3{x^2} + 6x + 4\) d) \(f\left( x \right) = - 2{x^2} + 3x + 5\) e) \(f\left( x \right) = - 6{x^2} + 3x - 1\) g) \(f\left( x \right) = 4{x^2} + 12x + 9\) Lời giải chi tiết a) \(f\left( x \right) = {x^2} - 5x + 4\) có \(\Delta = 9 > 0\) , hai nghiệm phân biết \({x_1} = 1,{x_2} = 4\) và có \(a = 1 > 0\) Ta có bảng xét dấu \(f\left( x \right)\) như sau:
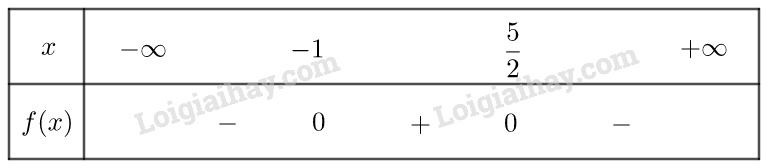
Vậy \(f\left( x \right)\) dương trong hai khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {4; + \infty } \right)\), âm trong khoảng \(\left( {1;4} \right)\) b) \(f\left( x \right) = - \frac{1}{3}{x^2} + 2x - 3\) có \(\Delta = 0\) , có nghiệm kép \({x_1} = {x_2} = 3\)và có \(a = - \frac{1}{3} < 0\) Vậy \(f\left( x \right)\) âm với mọi \(x \ne 3\) c) \(f\left( x \right) = 3{x^2} + 6x + 4\) có \(\Delta = - 12 < 0\) và có \(a = 3 > 0\) Vậy \(f\left( x \right)\) dương với mọi \(x \in \mathbb{R}\) d) \(f\left( x \right) = - 2{x^2} + 3x + 5\) có \(\Delta = 49 > 0\) , hai nghiệm phân biết \({x_1} = - 1,{x_2} = \frac{5}{2}\) và có \(a = - 2 < 0\) Ta có bảng xét dấu \(f\left( x \right)\) như sau:
Vậy \(f\left( x \right)\) âm trong khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {\frac{5}{2}; + \infty } \right)\), dương trong khoảng \(\left( { - 1;\frac{5}{2}} \right)\) e) \(f\left( x \right) = - 6{x^2} + 3x - 1\) có \(\Delta = - 15 < 0\) và có \(a = - 6 < 0\) Vậy \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\) g) \(f\left( x \right) = 4{x^2} + 12x + 9\) có \(\Delta = 0\) , có nghiệm kép \({x_1} = {x_2} = - \frac{3}{2}\)và có \(a = 4 > 0\)
Vậy \(f\left( x \right)\) dương với mọi \(x \ne - \frac{3}{2}\) a) \(f\left( x \right) = {x^2} - 5x + 4\) có \(\Delta = 9 > 0\) , hai nghiệm phân biết \({x_1} = 1,{x_2} = 4\) và có \(a = 1 > 0\) Ta có bảng xét dấu \(f\left( x \right)\) như sau:
Vậy \(f\left( x \right)\) dương trong hai khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {4; + \infty } \right)\), âm trong khoảng \(\left( {1;4} \right)\) b) \(f\left( x \right) = - \frac{1}{3}{x^2} + 2x - 3\) có \(\Delta = 0\) , có nghiệm kép \({x_1} = {x_2} = 3\)và có \(a = - \frac{1}{3} < 0\) Vậy \(f\left( x \right)\) âm với mọi \(x \ne 3\) c) \(f\left( x \right) = 3{x^2} + 6x + 4\) có \(\Delta = - 12 < 0\) và có \(a = 3 > 0\) Vậy \(f\left( x \right)\) dương với mọi \(x \in \mathbb{R}\) d) \(f\left( x \right) = - 2{x^2} + 3x + 5\) có \(\Delta = 49 > 0\) , hai nghiệm phân biết \({x_1} = - 1,{x_2} = \frac{5}{2}\) và có \(a = - 2 < 0\) Ta có bảng xét dấu \(f\left( x \right)\) như sau:
Vậy \(f\left( x \right)\) âm trong khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {\frac{5}{2}; + \infty } \right)\), dương trong khoảng \(\left( { - 1;\frac{5}{2}} \right)\) e) \(f\left( x \right) = - 6{x^2} + 3x - 1\) có \(\Delta = - 15 < 0\) và có \(a = - 6 < 0\) Vậy \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\) g) \(f\left( x \right) = 4{x^2} + 12x + 9\) có \(\Delta = 0\) , có nghiệm kép \({x_1} = {x_2} = - \frac{3}{2}\)và có \(a = 4 > 0\) Vậy \(f\left( x \right)\) dương với mọi \(x \ne - \frac{3}{2}\)
|






















Danh sách bình luận