Giải bài 5 trang 85 sách bài tập toán 9 - Cánh diều tập 2Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau tại K. Tìm tâm đường tròn ngoại tiếp mỗi tam giác sau: a) Tam giác BDE; b) Tam giác DEC c) Tam giác ADE. Quảng cáo
Đề bài Cho tam giác nhọn ABC. Các đường cao BE, CD của tam giác ABC cắt nhau tại K. Tìm tâm đường tròn ngoại tiếp mỗi tam giác sau: a) Tam giác BDE; b) Tam giác DEC c) Tam giác ADE. Phương pháp giải - Xem chi tiết Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó. Tâm đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác của tam giác đó. Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền. Lời giải chi tiết
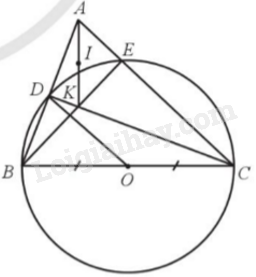
a) Gọi O là trung điểm của BC. Do tam giác BDC vuông ở D và BEC vuông ở E. Nên OB = OD = OC = OE (*). Do đó, O là tâm đường tròn ngoại tiếp tam giác BDE. b) Do (*), ta có O là tâm đường tròn ngoại tiếp tam giác DEC. c) Gọi I là trung điểm của AK. Do tam giác ADK vuông ở D và tam giác AEK vuông ở E nên IA = IK = IE = ID. Do đó, I là tâm đường tròn ngoại tiếp tam giác ADE.
|




















Danh sách bình luận