Giải bài 10 trang 86 sách bài tập toán 9 - Cánh diều tập 2Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm phân biệt A, B. Đường thẳng AO cắt (O) và (O’) lần lượt tại hai điểm C, E (khác điểm A). Đường thẳng AO’ cắt (O) và (O’) lần lượt tại hai điểm D, F (khác điểm A). Chứng minh: a) C, B, F thẳng hàng; b) Bốn điểm C, D, E, F cùng nằm trên một đường tròn; c) A là tâm đường tròn nội tiếp tam giác BDE. Quảng cáo
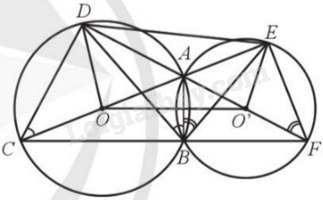
Đề bài Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm phân biệt A, B. Đường thẳng AO cắt (O) và (O’) lần lượt tại hai điểm C, E (khác điểm A). Đường thẳng AO’ cắt (O) và (O’) lần lượt tại hai điểm D, F (khác điểm A). Chứng minh: a) C, B, F thẳng hàng; b) Bốn điểm C, D, E, F cùng nằm trên một đường tròn; c) A là tâm đường tròn nội tiếp tam giác BDE. Phương pháp giải - Xem chi tiết Chứng minh \(\widehat {ABC} = {90^o}\), \(\widehat {ABF} = {90^o}\) suy ra C, B, F thẳng hàng. Chứng minh tam giác CDF và tam giác CEF nội tiếp đường tròn đường kính CF. Chứng minh DA là tia phân giác của \(\widehat {BDE}\) suy ra A là tâm đường tròn nội tiếp tam giác BDE. Lời giải chi tiết
a) Do AC và AF lần lượt là đường kính của đường tròn (O) và (O’) nên \(\widehat {ABC} = {90^o}\), \(\widehat {ABF} = {90^o}\). Suy ra C, B, F thẳng hàng. b) Ta có tam giác CDF và tam giác CEF nội tiếp đường tròn đường kính CF. Nên 4 điểm C, D, E, F cùng nằm trên một đường tròn. c) Ta có: \(\widehat {DCA} = \widehat {DBA}\) (hai góc nội tiếp cùng chắn cung DA của đường tròn (O)) (1). Tương tự \(\widehat {ABE} = \widehat {AFE}\) và \(\widehat {DCE} = \widehat {DFE}\) (2). Từ (1) và (2) suy ra \(\widehat {ABE} = \widehat {DBA}\), do đó BA là phân giác của góc DBE. Ta có: \(\widehat {ADB} = \widehat {ACB}\) (hai góc nội tiếp cùng chắn cung AB của đường tròn (O)) (3). Vì C, D, E, F cùng thuộc một đường tròn nên CDEF là tứ giác nội tiếp. Do đó \(\widehat {ECF} = \widehat {EDF}\) (hai góc nội tiếp cùng chắn cung EF của đường tròn ngoại tiếp CDEF) hay \(\widehat {ACB} = \widehat {EDA}\) (4). Từ (3) và (4) suy ra \(\widehat {ADB} = \widehat {EDA}\), do đó DA là phân giác của góc BDE. Mà BA cắt DA tại A nên A là tâm đường tròn nội tiếp tam giác BDE.
|




















Danh sách bình luận