Giải bài 4 trang 94 sách bài tập toán 10 - Chân trời sáng tạoCho hình bình hành ABCD có tâm O. Chứng minh rằng: Quảng cáo
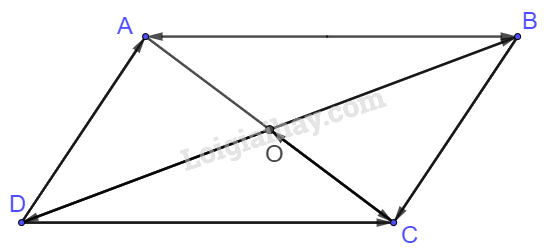
Đề bài Cho hình bình hành ABCD có tâm O. Chứng minh rằng: a) \(\overrightarrow {CO} - \overrightarrow {OB} = \overrightarrow {BA} \) b) \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {DB} \) c) \(\overrightarrow {DA} - \overrightarrow {DB} = \overrightarrow {OD} - \overrightarrow {OC} \) d) \(\overrightarrow {DA} - \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \) Phương pháp giải - Xem chi tiết Sử dụng tính chất của phép cộng, trừ vectơ và quy tắc ba điểm Lời giải chi tiết
a) Hình bình hành ABCD có tâm O nên \(\overrightarrow {CO} = \overrightarrow {OA} ,\overrightarrow {AB} = \overrightarrow {DC} ,\overrightarrow {BC} = \overrightarrow {AD} \) \(\overrightarrow {CO} - \overrightarrow {OB} = \overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \) (đpcm) b) \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {DC} - \overrightarrow {BC} = \overrightarrow {DC} + \overrightarrow {CB} = \overrightarrow {DB} \) (đpcm) c) Ta có: \(\begin{array}{l}\overrightarrow {DA} - \overrightarrow {DB} = \overrightarrow {BA} \\\overrightarrow {OD} - \overrightarrow {OC} = \overrightarrow {CD} \end{array}\) Mặt khác ta có \(\overrightarrow {BA} = \overrightarrow {CD} \), suy ra \(\overrightarrow {DA} - \overrightarrow {DB} = \overrightarrow {OD} - \overrightarrow {OC} \) (đpcm) d) \(\overrightarrow {DA} - \overrightarrow {DB} + \overrightarrow {DC} = \left( {\overrightarrow {DA} - \overrightarrow {DB} } \right) + \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {DC} \) Mà ta có ABCD là hình bình hành nên \(\overrightarrow {BA} \) và \(\overrightarrow {DC} \) là hai vectơ đối nhau \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow 0 \Rightarrow \overrightarrow {DA} - \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \) (đpcm)
|




















Danh sách bình luận