Giải bài 4 trang 92, 93 vở thực hành Toán 9 tập 2Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng (widehat {EIF} + widehat {BAC} = {180^o}). Quảng cáo
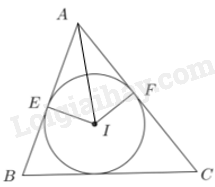
Đề bài Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng \(\widehat {EIF} + \widehat {BAC} = {180^o}\). Phương pháp giải - Xem chi tiết + Chứng minh \(\widehat {EIA} + \widehat {IAE} = {90^o}\) và \(\widehat {FAI} + \widehat {AIF} = {90^o}\). + \(\widehat {EIF} + \widehat {BAC} = \widehat {EIA} + \widehat {FIA} + \widehat {IAF} + \widehat {IAE}\) \(= \left( {\widehat {EIA} + \widehat {IAE}} \right) + \left( {\widehat {FAI} + \widehat {AIF}} \right)\), suy ra điều phải chứng minh. Lời giải chi tiết
Vì các tam giác EIA và FIA lần lượt vuông tại đỉnh E và F nên \(\widehat {EIA} + \widehat {IAE} = {90^o}\) và \(\widehat {FAI} + \widehat {AIF} = {90^o}\). Ta có: \(\begin{array}{l}\widehat {EIF} + \widehat {BAC} = \widehat {EIA} + \widehat {FIA} + \widehat {IAF} + \widehat {IAE}\\ = \left( {\widehat {EIA} + \widehat {IAE}} \right) + \left( {\widehat {FAI} + \widehat {AIF}} \right)\\ = {90^o} + {90^o} = {180^o}\end{array}\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
