Giải bài 4 trang 87 SGK Toán 8 tập 1– Chân trời sáng tạoCho tam giác Quảng cáo
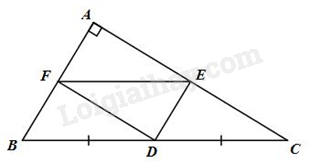
Đề bài Cho tam giác \(ABC\) vuông tại \(A\) (\(AB < AC\). Gọi \(D\) là trung điểm của \(BC\). Vẽ \(DE\) // \(AB\), vẽ \(DF\) // \(AC\) \((E \in AC\); \(F \in AB)\). Chứng minh rằng: a) Tứ giác \(AEDF\) là hình chữ nhật b) Tứ giác \(BFED\) là hình bình hành Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Áp dụng dấu hiệu nhận biết hình chữ nhật b) Áp dụng dấu hiệu nhận biết hình bình hành Lời giải chi tiết
a) Ta có: \(\Delta ABC\) vuông tại \(A\) nên \(\widehat {{\rm{BAC}}} = 90^\circ \) và \(AB \bot AC\) Mà \(DE\) // \(AB\) ; \(DF\) // \(AC\) Suy ra \(DE \bot AC;\;DF \bot AB\) Suy ra \(\widehat {DEA} = \widehat {DFA} = 90^\circ \) Tứ giác \(AEDF\) có \(\widehat {BAC} = \widehat {DEA} = \widehat {DFA} = 90^\circ \) nên là hình chữ nhật b) Vì \(AEDF\) là hình chữ nhật (cmt) Suy ra \(AE = DF\); \(AF = DE\); \(AF\) // \(DE\); \(AE\) // \(DF\) Vì \(DE \bot AC;\;DF \bot AB\) (cmt) Suy ra \(\widehat {DEC} = \widehat {BFD} = 90^\circ \) Xét \(\Delta BFD\) và \(\Delta DEC\) ta có: \(\widehat {{\rm{BFD}}} = \widehat {{\rm{DEC}}} = 90^\circ \) (cmt) \(BD = DC\) (gt) \(\widehat {{\rm{FBD}}} = \widehat {{\rm{EDC}}}\) (do \(DE\) // \(BF\) ) Suy ra \(\Delta BFD = \Delta DEC\) (ch – gn) Suy ra \(BF = DE\); \(DF = EC\) (hai cạnh tương tứng) Xét tứ giác \(BFED\) ta có: \(BF\) // \(DE\) (do \(AB\) // \(DE\)) \(BF = DE\) (cmt) Suy ra \(BFED\) là hình bình hành
|




















Danh sách bình luận