Giải bài 3.7 trang 55 SGK Toán 8 tập 1 - Kết nối tri thức

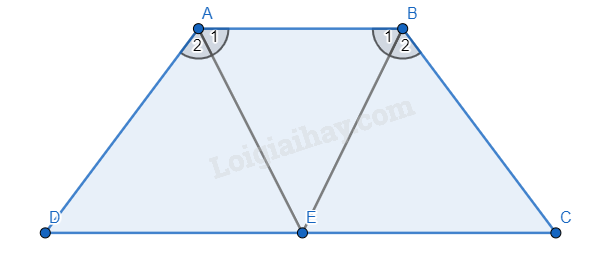
Đề bài

Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.

Lời giải chi tiết

Vì ABCD là hình thang cân nên $\widehat {DAB} = \widehat {ABC};\widehat C = \widehat D;A{\rm{D}} = BC$

Theo đề bài, ta có AE, BE lần lượt là tia phân giác của $\widehat {BA{\rm{D}}}$ và $\widehat {ABC}$

Suy ra $\widehat {{A_1}} = \widehat {{A_2}};\widehat {{B_1}} = \widehat {{B_2}}$

Mà $\widehat {DAB} = \widehat {ABC}$ nên $\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}}$

Xét ∆ADE và ∆BCE có:

$\widehat {{A_2}} = \widehat {{B_2}}$ (chứng minh trên)

AD = BC (chứng minh trên)

$\widehat {{D}} = \widehat {{C}}$ (chứng minh trên)

Do đó ∆ADE = ∆BCE (g.c.g).

Suy ra EC = ED (hai cạnh tương ứng).