Giải bài 35 trang 117 sách bài tập toán 9 - Cánh diều tập 1Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40m và chiều cao MK = 6m (Hình 35). Tính bán kính của đường tròn chứa cung AMB (làm tròn kết quả đến hàng phần mười của mét). Quảng cáo
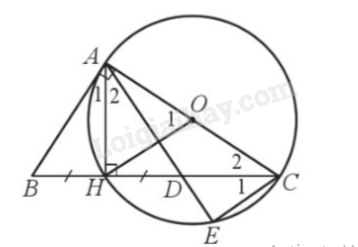
Đề bài Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm O đường kính AC. Trên tia BH, lấy điểm D sao cho H là trung điểm của đoạn thẳng BD. Nối A với D cắt đường tròn (O) tại E. Chứng minh: a) CH là tia phân giác của góc ACE; b) OH // EC. Phương pháp giải - Xem chi tiết a) Bước 1: Chứng minh \(\widehat {{A_1}} = \widehat {{C_1}}\) (vì cùng bằng \(\widehat {{A_2}}\)) Bước 2: Chứng minh \(\widehat {{A_1}} = \widehat {{C_2}}\) (cùng phụ với góc B). b) Chứng minh 2 góc đồng vị bằng nhau \(\widehat {{O_1}} = 2\widehat {{C_2}}\)(góc ở tâm bằng số đo cung bị chắn, góc nội tiếp bằng nửa số đo cung bị chắn). Lời giải chi tiết
a) Ta có \(\widehat {{A_2}} = \widehat {{C_1}}\) (góc nội tiếp chắn cung HE của (O)). Xét \(\Delta ABD\)có \(AH \bot BD,BH = DH\), hay AH vừa là đường cao, vừa là đường trung tuyến, nên tam giác ABD cân tại A, do đó AH đồng thời là đường phân giác, suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\). Vậy \(\widehat {{A_1}} = \widehat {{C_1}}\) (1) Mặt khác \(\widehat {{A_1}} + \widehat B = 90^\circ \) (do tam giác AHB vuông tại H), \(\widehat {{C_2}} + \widehat B = 90^\circ \) (do tam giác ACB vuông tại A). Do đó \(\widehat {{A_1}} = \widehat {{C_2}}\) (2) Từ (1) và (2) suy ra \(\widehat {{C_2}} = \widehat {{C_1}}\) hay CH là tia phân giác của góc ACE. b) Ta có \(\widehat {{O_1}}\) là góc ở tâm và \(\widehat {{C_2}}\) là góc nội tiếp cùng chắn cung AH của (O) nên \(\widehat {{O_1}} = 2\widehat {{C_2}}\)= \(\widehat {ACE}\) = sđ\(\overset\frown{AH}\). Mà \(\widehat {{O_1}};\widehat {ACE}\) là 2 góc đồng vị nên OH // EC.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
