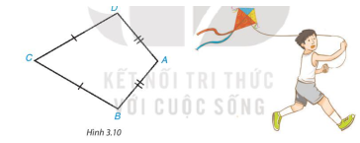
Giải bài 3.3 trang 50 SGK Toán 8 tập 1 - Kết nối tri thức

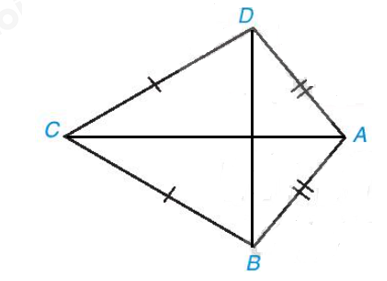
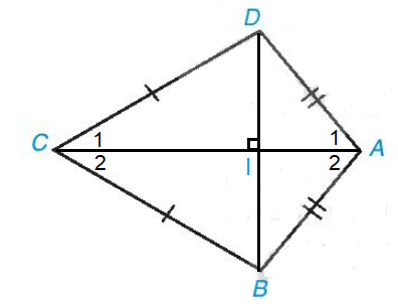
Đề bài

Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.

a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.

b) Tính các góc B, D biết rằng $\widehat A$=100°,$\widehat C$=60°

Lời giải chi tiết

a) Nối AC, BD (như hình vẽ

Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;

CB = CD hay hai điểm C cách đều hai đầu mút B và D;

Do đó, hai điểm A và C cách đều hai đầu mút B và D.

Vậy AC là đường trung trực của đoạn thẳng BD.

b) Gọi I là giao điểm của AC và BD.

Vì AC là đường trung trực của đoạn thẳng BD nên AC ⊥ BD.

• Xét tam giác ABD cân tại A (vì AB = AD) có AI là đường cao (vì AI ⊥ BD)

Nên AI cũng là tia phân giác của $\widehat {BA{\rm{D}}}$ hay $\widehat {{A_1}} = \widehat {{A_2}}$

Suy ra $\widehat {{A_1}} = \widehat {{A_2}} = \widehat {B{\rm{D}}A}:2 = {100^o}:2 = {50^o}$

• Xét tam giác BCD cân tại C (vì BC = CD) có CI là đường cao (vì AC ⊥ BD)

Nên CI cũng là tia phân giác của $\widehat {BC{\rm{D}}}$ hay $\widehat {{C_1}} = \widehat {{C_2}}$

Suy ra $\widehat {{C_1}} = \widehat {{C_2}} = \widehat {BC{\rm{D}}}:2 = {60^o}:2 = {30^o}$

• Xét tam giác ACD có: $\widehat {{A_1}} + \widehat {{C_1}} + \widehat {A{\rm{D}}C} = {180^o}$ (định lí tổng ba góc trong một tam giác).

Hay 50°+30°+$\widehat {A{\rm{D}}C}$=180°

Suy ra $\widehat {A{\rm{D}}C}$=180°−50°−30°=100°

Xét tứ giác ABCD có:

$\widehat {BA{\rm{D}}} + \widehat {ABC} + \widehat {BC{\rm{D}}} + \widehat {A{\rm{D}}C} = {360^o}$(định lí tổng bốn góc của một tứ giác).

Hay 100°+$\widehat {ABC}$+60°+100°=360°

Suy ra $\widehat {ABC}$+260°=360^o

Do đó $\widehat {ABC}$=360°−260°=100^o

Vậy $\widehat {ABC}$=100° ;$\widehat {A{\rm{D}}C}$=100°