Giải bài 3.22 trang 69 sách bài tập toán 12 - Kết nối tri thứcMột người đầu tư cùng một số tiền vào hai lĩnh vực A và B. Nhà đầu tư này ghi lại số tiền thu được hằng tháng trong hai năm theo mỗi lĩnh vực cho kết quả như sau: Tính độ lệch chuẩn của hai mẫu số liệu ghép nhóm và nhận xét về mức độ ổn định của số tiền thu được hằng tháng khi đầu tư vào hai lĩnh vực trên. Quảng cáo
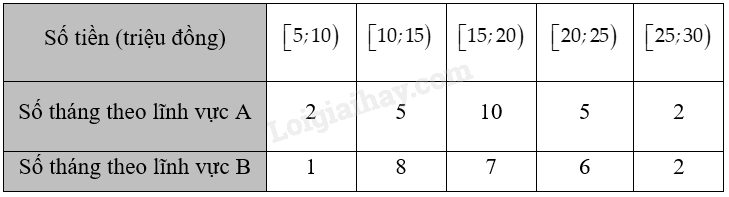
Đề bài Một người đầu tư cùng một số tiền vào hai lĩnh vực A và B. Nhà đầu tư này ghi lại số tiền thu được hằng tháng trong hai năm theo mỗi lĩnh vực cho kết quả như sau:
Tính độ lệch chuẩn của hai mẫu số liệu ghép nhóm và nhận xét về mức độ ổn định của số tiền thu được hằng tháng khi đầu tư vào hai lĩnh vực trên. Phương pháp giải - Xem chi tiết Xét từng mẫu số liệu ghép nhóm, sử dụng các công thức đã học để tìm số trung bình và độ lệch chuẩn của chúng. So sánh hai giá trị độ lệch chuẩn để rút ra nhận xét về mức độ ổn định của số tiền thu được hằng tháng khi đầu tư vào hai lĩnh vực. Lời giải chi tiết + Xét mẫu số liệu về số tiền thu được hằng tháng trong hai năm theo lĩnh vực A: Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:
Cỡ mẫu là \(n = 24\). Giá trị trung bình của mẫu số liệu là \(\overline {{x_A}} = \frac{{7,5 \cdot 2 + 12,5 \cdot 5 + 17,5 \cdot 10 + 22,5 \cdot 5 + 27,5 \cdot 2}}{{24}} = \frac{{420}}{{24}} = 17,5\). Độ lệch chuẩn của mẫu số liệu là \(\begin{array}{l}{s_A} = \sqrt {\frac{1}{n}\left( {{{7,5}^2} \cdot 2 + {{12,5}^2} \cdot 5 + {{17,5}^2} \cdot 10 + {{22,5}^2} \cdot 5 + {{27,5}^2} \cdot 2} \right) - {{\left( {\overline {{x_A}} } \right)}^2}} \\{\rm{ }} = \sqrt {\frac{{8000}}{{24}} - {{17,5}^2}} = \sqrt {\frac{{325}}{{12}}} \approx 5,2042.\end{array}\) + Xét mẫu số liệu về số tiền thu được hằng tháng trong hai năm theo lĩnh vực A: Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:
Cỡ mẫu là \(m = 24\). Giá trị trung bình của mẫu số liệu là \(\overline {{x_B}} = \frac{{7,5 \cdot 1 + 12,5 \cdot 8 + 17,5 \cdot 7 + 22,5 \cdot 6 + 27,5 \cdot 2}}{{24}} = \frac{{420}}{{24}} = 17,5\). Độ lệch chuẩn của mẫu số liệu là \(\begin{array}{l}{s_B} = \sqrt {\frac{1}{m}\left( {{{7,5}^2} \cdot 1 + {{12,5}^2} \cdot 8 + {{17,5}^2} \cdot 7 + {{22,5}^2} \cdot 6 + {{27,5}^2} \cdot 2} \right) - {{\left( {\overline {{x_B}} } \right)}^2}} \\{\rm{ }} = \sqrt {\frac{{8000}}{{24}} - {{17,5}^2}} = \sqrt {\frac{{325}}{{12}}} \approx 5,2042.\end{array}\) Ta có \({x_A} = {x_B}\) và \({s_A} = {s_B}\). Suy ra giá trị trung bình và độ lệch chuẩn của hai mẫu số liệu giống nhau. Do độ lệch chuẩn bằng nhau nên mức độ ổn định của hai phương án đầu tư là như nhau.
|






















Danh sách bình luận