Giải bài 3 trang 122 sách bài tập toán 10 - Chân trời sáng tạoTổng lượng mưa trong năm tại một trạm quan trắc đặt tại Nha Trang từ 2010 đến 2020 được thể hiện trong biểu đồ sau ( đơn vị: mm). Quảng cáo
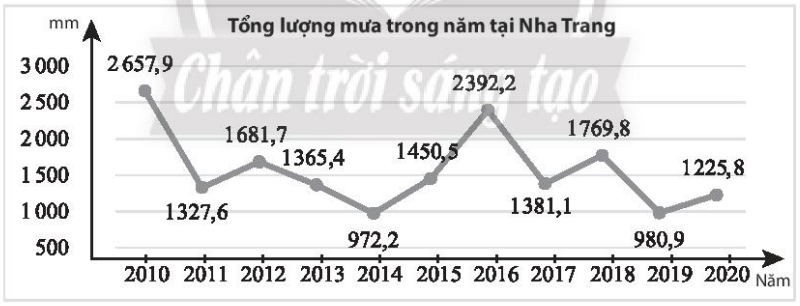
Đề bài Tổng lượng mưa trong năm tại một trạm quan trắc đặt tại Nha Trang từ 2010 đến 2020 được thể hiện trong biểu đồ sau (đơn vị: mm).
a) Hãy tính lượng mưa trung bình tại trạm quan trắc trên từ 2010 đến 2020. b) Hãy tìm các tứ phân vị của mẫu số liệu đó. Phương pháp giải - Xem chi tiết - Dùng công thức tính số trung bình: \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\) - Bước 1: Sắp xếp các số liệu theo thứ tự không giảm. Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu). Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ) Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ) Lời giải chi tiết a) Lượng mưa trung bình tại trạm quan trắc trên từ 2010 đến 2020 là: \(\overline x = \frac{{2657,9 + 1327,6 + 1681,7 + 1365,4 + 972,2 + 1450,5 + 2392,2 + 1381,1 + 1769,8 + 980,9 + 1225,8}}{{11}} = 1564,1\) b) Sắp xếp số liệu theo thứ tự không giảm ta được: 972,2 ;980,9; 1225,8; 1327,6; 1365,4; 1381,1; 1450,5; 1681,7; 1769,8; 2392,2; 2657,9. Vì \(n = 11\)là số lẻ nên \({Q_2} = 1381,1\) Tứ phân vị thứ nhất là trung vị của 5 số đầu \({Q_1} = 1225,8\) Tứ phân vị thứ ba là trung vị của 5 số cuối \({Q_3} = 1769,8\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
