Giải bài 26 trang 114 sách bài tập toán 9 - Cánh diều tập 2Cho ngũ giác đều ABCDE. Về phía ngoài của ngũ giác đó dựng tam giác đều PDE (Hình 24). Tính số đo góc APC. Quảng cáo
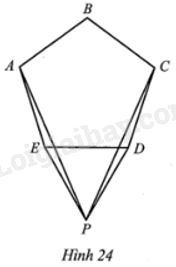
Đề bài Cho ngũ giác đều ABCDE. Về phía ngoài của ngũ giác đó dựng tam giác đều PDE (Hình 24). Tính số đo góc APC.
Phương pháp giải - Xem chi tiết Dựa vào: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau. Lời giải chi tiết Tổng số đo tất cả các góc của ngũ giác ABCDE bằng tổng số đo các góc của tam giác ABE và tứ giác BCDE, và bằng: 180° + 360° = 540°. Do ABCDE là ngũ giác đều suy ra các góc của nó đều bằng nhau và bằng \(\frac{{{{540}^o}}}{5} = {108^o}\). Do PDE là tam giác đều nên PE = PD = DE và \(\widehat {PDE} = \widehat {PED} = \widehat {EPD} = {60^o}\). Do đó: \(\widehat {AEP} = \widehat {AED} + \widehat {DEP} = {180^o} + {60^o} = {168^o}\); \(\widehat {CDP} = \widehat {CDE} + \widehat {EDP} = {180^o} + {60^o} = {168^o}\). Do ABCDE là ngũ giác đều suy ra DE = EA = DC. Do đó PE = PD = DE = EA = DC nên các tam giác EAP, DCP là các tam giác cân lần lượt tại các đỉnh E và D. Suy ra: \(\widehat {EPA} = \frac{{{{180}^o} - \widehat {AEP}}}{2} = \frac{{{{180}^o} - {{168}^o}}}{2} = {6^o}\); \(\widehat {DPC} = \frac{{{{180}^o} - \widehat {CDP}}}{2} = \frac{{{{180}^o} - {{168}^o}}}{2} = {6^o}\). Vì vậy ta có \(\widehat {APC} = \widehat {EPD} - \widehat {EPA} - \widehat {DPC}\) \(= {60^o} - {6^o} - {6^o} = {48^o}\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
