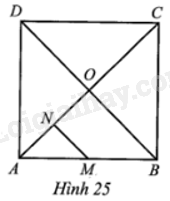
Giải bài 31 trang 115 sách bài tập toán 9 - Cánh diều tập 2Cho hình vuông ABCD và O là giao điểm của AC và BD. Gọi M là trung điểm của AB, N là trung điểm của AO (Hình 25). Phép quay ngược chiều 90° tâm O biến các điểm N, M lần lượt thành các điểm N’, M’. a) Chứng minh tam giác BN'M' là tam giác vuông cân. b) Tính tỉ số diện tích tam giác ANM và diện tích tam giác CN'M'. c) Phát biểu “Phép quay thuận chiều 90° tâm N biến điểm O thành điểm M, biến điểm D thành điểm B” là đúng hay sai? Vì sao? Quảng cáo
Đề bài Cho hình vuông ABCD và O là giao điểm của AC và BD. Gọi M là trung điểm của AB, N là trung điểm của AO (Hình 25). Phép quay ngược chiều 90° tâm O biến các điểm N, M lần lượt thành các điểm N’, M’. a) Chứng minh tam giác BN'M' là tam giác vuông cân. b) Tính tỉ số diện tích tam giác ANM và diện tích tam giác CN'M'. c) Phát biểu “Phép quay thuận chiều 90° tâm N biến điểm O thành điểm M, biến điểm D thành điểm B” là đúng hay sai? Vì sao?
Phương pháp giải - Xem chi tiết Chứng minh BN’ = M’N’ và \(\widehat {BN'M'} = {90^o}\) nên BN'M' là tam giác vuông cân. Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo \({\alpha ^o}\). Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O được phát biểu tương tự như trên. Lời giải chi tiết
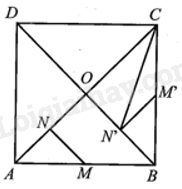
a) Do phép quay ngược chiều 90° tâm O biến các điểm N, M lần lượt thành các điểm N’, M’ nên ON = ON’, OM = OM’ và \(\widehat {NON'} = \widehat {MOM'} = {90^o}\). Do đó các tam giác ONN’ và OMM’ là các tam giác vuông cân tại O. Do ABCD là hình vuông tâm O nên OA = OB = OC = OD. Ta có OA = 2ON nên OB = OA = 2ON = 2ON’, do đó N’ là trung điểm của OB. Suy ra AN = \(\frac{1}{2}OA = \frac{1}{2}OB = BN'\). Xét ∆OAB vuông tại O có OM là đường trung tuyến ứng với cạnh huyền AB nên OM = \(\frac{1}{2}AB\), mà AB = BC và OM = OM’ nên \(OM' = \frac{1}{2}BC\). Xét ∆OBC vuông tại O có \(OM' = \frac{1}{2}BC\) nên OM’ là đường trung tuyến ứng với cạnh huyền hay M’ là trung điểm của BC. Suy ra \(AM = \frac{1}{2}AB = \frac{1}{2}BC = BM'\). Xét ∆ANM và ∆BN’M’ có: AN = BN’, \(\widehat {MAN} = \widehat {M'BN'} = {45^o}\), AM = BM’. Do đó ∆ANM = ∆BN’M’ (c.g.c). Suy ra MN = M’N’ (hai cạnh tương ứng) và \(\widehat {ANM} = \widehat {BM'N'}\) (hai góc tương ứng). Xét ∆OAB có N, M lần lượt là trung điểm của AO, AB nên NM là đường trung bình của tam giác, do đó NM // OB và NM = \(\frac{1}{2}OB\). Ta có MN = M’N’ và BN’ = \(\frac{1}{2}OB\)= NM nên BN’ = M’N’. Lại có NM // OB và OB ⊥ AO nên NM ⊥ AO hay \(\widehat {ANM} = {90^o}\), suy ra \(\widehat {BN'M'} = {90^o}\) Tam giác BN’M’ có BN’ = M’N’ và \(\widehat {BN'M'} = {90^o}\)nên là tam giác vuông cân tại N’. b) Kí hiệu diện tích các tam giác ANM, AOB, CN’M’, CN’B, COB lần lượt là SANM, SAOB, SCN’M’, SCN’B, SCOB. Gọi hN’ là chiều cao kẻ từ N’ đến BC. Ta có: \({S_{ANM}} = \frac{1}{2}AN.MN = \frac{1}{4}.\left( {\frac{1}{2}OA.OB} \right) = \frac{1}{4}{S_{AOB}}\); \({S_{CN'M'}} = \frac{1}{2}{h_{N'}}.CM = \frac{1}{2}.\left( {\frac{1}{2}{h_{N'}}.BC} \right) = \frac{1}{2}{S_{CN'B}}\) \({S_{CN'B}} = \frac{1}{2}CO.N'B = \frac{1}{2}.\left( {\frac{1}{2}.CO.OB} \right) = \frac{1}{2}{S_{COB}}\). Suy ra \({S_{CN'M'}} = \frac{1}{2}{S_{CN'B}} = \frac{1}{2}.\frac{1}{2}{S_{COB}} = \frac{1}{4}{S_{COB}}\). Mặt khác, \({S_{AOB}} = \frac{1}{2}.OA.OB = \frac{1}{2}.OC.OB = {S_{COB}}\). Do đó: \({S_{ANM}} = {S_{CN'M'}}\). Vậy \({S_{ANM}}:{S_{CN'M'}} = 1\). c) Ta có AC ⊥ BD tại trung điểm O của BD nên AO là đường trung trực của BC. Mà N ∈ AC nên ND = NB. Do đó tam giác NDB cân ở N và dễ thấy rằng \(\widehat {DNB} > {90^o}\). Suy ra phép quay thuận chiều 90° tâm N không thể biến điểm D thành điểm B. Vậy phát biểu “Phép quay thuận chiều 90° tâm N biến điểm O thành điểm M, biến điểm D thành điểm B” là sai.
|




















Danh sách bình luận