Giải bài 2.3 trang 44 sách bài tập toán 12 - Kết nối tri thứcCho hình hộp chữ nhật ABCD.A’B’C’D’ có (AB = AD = 1) và (AA' = 2). Tính độ dài của các vectơ sau: a) (overrightarrow {BD} )?; b) (overrightarrow {CD'} )? ; c) (overrightarrow {AC'} )?. Tổng hợp đề thi giữa kì 1 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
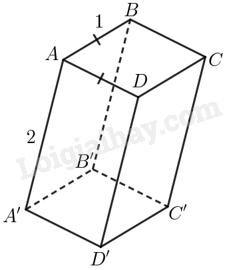
Đề bài Cho hình hộp chữ nhật ABCD.A’B’C’D’ có \(AB = AD = 1\) và \(AA' = 2\). Tính độ dài của các vectơ sau: a) \(\overrightarrow {BD} \) b) \(\overrightarrow {CD'} \) c) \(\overrightarrow {AC'} \) Phương pháp giải - Xem chi tiết Sử dụng tính chất của hình hộp chữ nhật về đáy, mặt bên, tính chất vuông góc. Ý a: Xác định tam giác vuông trong hình có chứa cạnh BD đã biết số đo hai cạnh còn lại sau đó áp dụng định lý Pythagore để tính độ dài BD. Ý b: Xác định tam giác vuông trong hình có chứa cạnh CD đã biết số đo hai cạnh còn lại sau đó áp dụng định lý Pythagore để tính độ dài CD. Ý c: Xác định tam giác vuông trong hình có chứa cạnh AC’ đã biết số đo hai cạnh còn lại sau đó áp dụng định lý Pythagore để tính độ dài AC’. Lời giải chi tiết
a) Xét tam giác vuông cân ABD ta có \(BD = \left| {\overrightarrow {BD} } \right| = \sqrt {A{B^2} + A{D^2}} = \sqrt {1 + 1} = \sqrt 2 \). b) Xét tam giác vuông cân CDD’ ta có \(BD' = \overrightarrow {\left| {BD'} \right|} = \sqrt {D{C^2} + D{{D'}^2}} = \sqrt {1 + 4} = \sqrt 5 \). c) Ta có tứ giác ABCD là hình vuông có cạnh bằng 1, suy ra \(AC = \left| {\overrightarrow {AC} } \right| = \sqrt {1 + 1} = \sqrt 2 \). Xét tam giác vuông ACC’ có \(AC' = \left| {\overrightarrow {AC'} } \right| = \sqrt {A{C^2} + C{{C'}^2}} = \sqrt {2 + 4} = \sqrt 6 \).  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
