Giải bài 2 trang 59 Chuyên đề học tập Toán 10 – Cánh diều

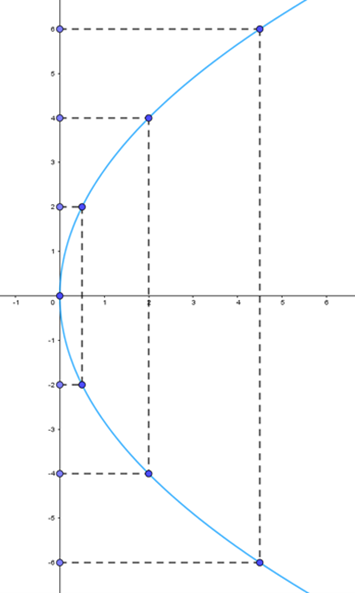
Đề bài

Trong mặt phẳng tọa độ Oxy, cho parabol có phương trình chính tắc là \({y^2} = 8x\)

a) Xác định tọa độ tiêu điểm và phương trình đường chuẩn của parabol

b) Vẽ parabol

Lời giải chi tiết

a) Ta có: \(2p = 8 \Rightarrow p = 4\)

Tiêu điểm của parabol (P) là \(F\left( {2;0} \right)\)

Đường chuẩn: \(\Delta :x =  - 2\)

b) Vẽ parabol

Để vẽ parabol (P): \({y^2} = 4x\) ta có thể làm như sau:

Bước 1: Lập bảng giá trị

x	0	0,5	0,5	2	2	4,5	4,5
y	0	-2	2	-4	4	-6	6

Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau

Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị

Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2