Giải bài 2 trang 108 vở thực hành Toán 9Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng: a) Đường tròn đường kính BC đi qua các điểm H và K; b) (KH < BC). Tổng hợp đề thi giữa kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN Quảng cáo
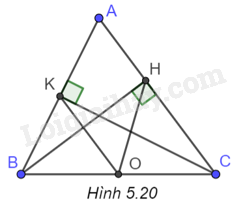
Đề bài Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng: a) Đường tròn đường kính BC đi qua các điểm H và K; b) \(KH < BC\). Phương pháp giải - Xem chi tiết a) Gọi O là trung điểm của BC. Chứng minh \(OH = OK = \frac{1}{2}BC\) nên đường tròn đường kính BC đi qua các điểm H và K. b) Trong một đường tròn, đường kính là dây cung lớn nhất. Lời giải chi tiết (H.5.20)
a) Gọi O là trung điểm của BC. Do \(\widehat {BHC} = \widehat {BKC} = {90^o}\) nên các tam giác BKC, BHC lần lượt vuông tại K và H. Ta có: \(OH = OK = \frac{1}{2}BC\). Do đó, đường tròn đường kính BC đi qua các điểm H và K. b) Theo câu a, HK là dây của đường tròn đường kính BC. Do đó, \(KH < BC\).
|




















Danh sách bình luận