Giải bài 16 trang 30 SBT toán 10 - Cánh diều

Đề bài

Viết hệ bất phương trình bậc nhất hai ẩn có miền nghiệm là miền đa giác không bị gạch ở mỗi Hình 10a, 10b

a)	b)
Hình 10

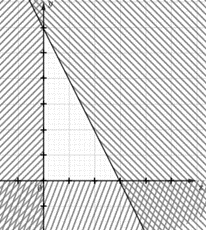
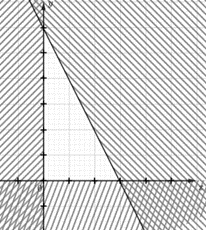
Lời giải chi tiết

Xét Hình 10a):

 

Ta có: Đường thẳng \({d_1}\) đi qua hai điểm O và A là trục tung Oy có phương trình x=0

Ta thấy điểm B thuộc miền nghiệm nằm bên phải trục tung nên điểm B thỏa mãn bất phương trình x ≥ 0 (1)

Đường thẳng d₂ đi qua hai điểm O và B là trục hoành Ox có phương trình y = 0.

Ta thấy điểm B thuộc miền nghiệm nằm trên trục hoành nên điểm B thỏa mãn bất phương trình y ≥ 0 (2)

Đường thẳng d₃ đi qua hai điểm A(0; 6) và B(3; 0) có phương trình là:

\(\frac{x}{3} + \frac{y}{6} = 1 \Leftrightarrow 2x + y = 6\)

Ta thấy điểm \(O\left( {0;0} \right)\) có 2.0 + 0 = 0 < 6 thuộc miền nghiệm nên điểm O thỏa mãn bất phương trình 2x + y ≤ 6 (3).

Từ (1), (2) và (3) miền nghiệm tam giác OAB biểu diễn cho hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{2x + y \le 6}\end{array}} \right.\)

Xét Hình 10b):

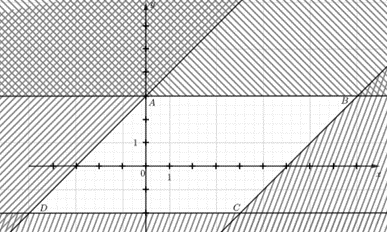
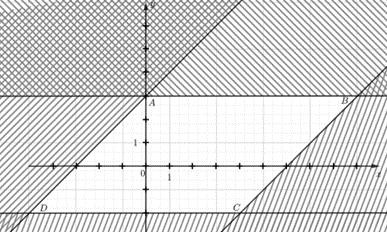
Ta có: Đường thẳng d₁ đi qua hai điểm A(0; 3) và B(9; 3) song song với trục hoành có phương trình y = 3.

Ta thấy điểm O thuộc miền nghiệm có 0 < 3 nên điểm O thỏa mãn bất phương trình y ≤ 3 (1)

Đường thẳng d₂ đi qua hai điểm A(0; 3) và D(– 5; – 2) cắt hai trục tọa độ Ox và Oy lần lượt tại các điểm có tọa độ là (– 3; 0) và (0; 3) có phương trình là: \(\frac{x}{{ - 3}} + \frac{y}{3} = 1 \Leftrightarrow x - y =  - 3\)

Ta thấy điểm O thuộc miền nghiệm có 0 – 0 = 0 > – 3 nên điểm O thỏa mãn bất phương trình x – y ≥ – 3.

Đường thẳng d₃ đi qua hai điểm B(9; 3) và C(4; – 2) song song với đường thẳng d₂ có phương trình là: x – y = c.

Vì đường thẳng này đi qua B(9; 3) nên ta có: 9 – 3 = c hay c = 6.

Khi đó phương trình d₃ là x – y = 6.

Ta thấy điểm O(0; 0) có 0 – 0 = 0 < 3 thuộc miền nghiệm nên điểm O thỏa mãn bất phương trình x – y ≤ 3 (3).

Đường thẳng d₁ đi qua hai điểm C(4; – 2) và D(– 5; – 2) song song với trục hoành có phương trình y = – 2.

Ta thấy điểm O thuộc miền nghiệm có 0 > – 2 nên điểm O thỏa mãn bất phương trình y ≥ – 2 (4)

Từ (1), (2), (3) và (4) miền nghiệm của tứ giác ABCD biểu diễn cho hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{y \le 3}\\{y \ge  - 2}\\{x - y \ge  - 3}\\{x - y \le 6}\end{array}} \right.\)