Giải bài 1.51 trang 28 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

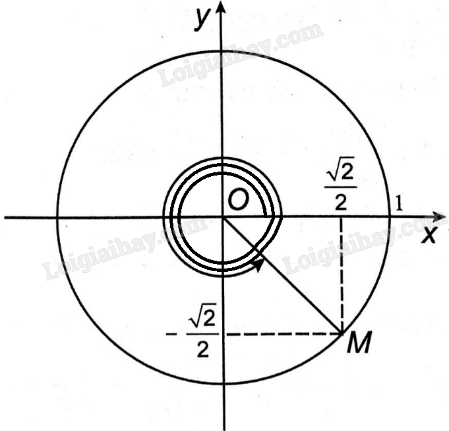
Đề bài

Trên đường tròn lượng giác, xác định điểm M  biểu diễn các góc lượng giác có số đo sau và tính các giá trị lượng giác của chúng:

a) \(\frac{{23\pi }}{4}\);                                

b) \(\frac{{31\pi }}{6}\);                   

c) \( - {1380^0}\).

Lời giải chi tiết

a) Ta có \(\frac{{23\pi }}{4} = 6\pi  - \frac{\pi }{4}\). Góc \(\frac{{23\pi }}{4}\)được biểu diễn bởi điểm M\(\left( {\frac{{\sqrt 2 }}{2}; - \frac{{\sqrt 2 }}{2}} \right)\) trên đường tròn lượng giác bên dưới.

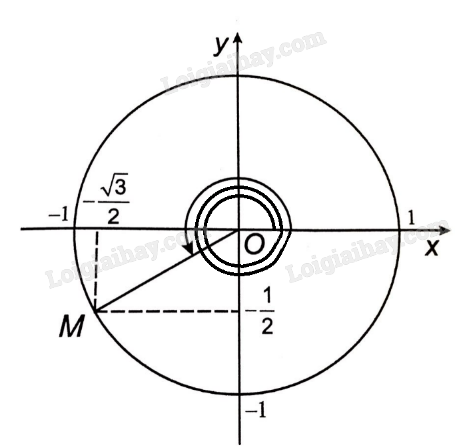
Vậy \(\sin \frac{{31\pi }}{6} = \,\, - \frac{1}{2},\cos \frac{{31\pi }}{6} = \, - \frac{{\sqrt 3 }}{2}\,,\tan \frac{{31\pi }}{6} = \,\frac{1}{{\sqrt 3 }}\,,\cot \frac{{31\pi }}{6} = \sqrt 3 \).

b) Ta có \(\frac{{31\pi }}{6} = 4\pi  + \frac{{7\pi }}{6}\). Góc \(\frac{{31\pi }}{6}\)được biểu diễn bởi điểm M\(\left( { - \frac{{\sqrt 3 }}{2}; - \frac{1}{2}} \right)\) trên đường tròn lượng giác bên dưới.

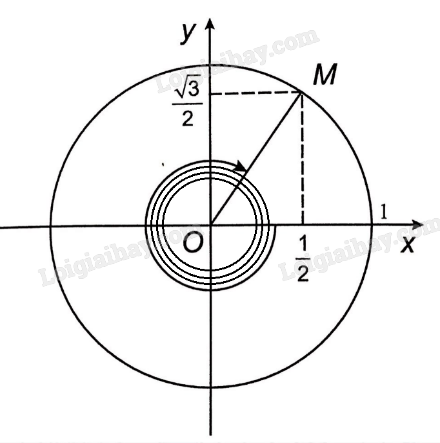
c) Ta có \( - {1380^0} =  - {4.360^0} + {60^0}\). Góc \( - {1380^0}\) được biểu diễn bởi điểm M\(\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)\) trên đường tròn lượng giác bên dưới.

Vậy \(\sin ( - {1380^0}) = \frac{{\sqrt 3 }}{2},\,\,\cos \,( - {1380^0}) = \frac{1}{2},\,\,\,\tan \,( - {1380^0}) = \sqrt 3 ,\,\,\cot \,( - {1380^0}) = \frac{1}{{\sqrt 3 }}.\)