Giải bài 15 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2Cho tam giác nhọn ABC (AB < AC) có hai đường cao BD và CE. a) Chứng minh bốn điểm B, C, D, E cùng thuộc đường tròn. b) Vẽ đường tròn (B; BD). Chứng minh AC là tiếp tuyến của đường tròn (B; BD). c) Đường tròn (B; BD) cắt CE tại K (K nằm giữa E và C). Qua D vẽ đường thẳng vuông góc với BC tại H và cắt đường thẳng AB tại M. Chứng minh (widehat {BMH} = widehat {BKH}). Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Quảng cáo
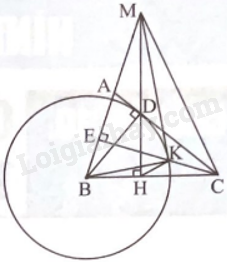
Đề bài Cho tam giác nhọn ABC (AB < AC) có hai đường cao BD và CE. a) Chứng minh bốn điểm B, C, D, E cùng thuộc đường tròn. b) Vẽ đường tròn (B; BD). Chứng minh AC là tiếp tuyến của đường tròn (B; BD). c) Đường tròn (B; BD) cắt CE tại K (K nằm giữa E và C). Qua D vẽ đường thẳng vuông góc với BC tại H và cắt đường thẳng AB tại M. Chứng minh \(\widehat {BMH} = \widehat {BKH}\). Phương pháp giải - Xem chi tiết Chứng minh tam giác BEC và tam giác BDC nội tiếp đường tròn đường kính BC. Từ đó suy ra bốn điểm B, C, D, E cùng thuộc đường tròn đường kính BC. Chứng minh BD \( \bot \)AC tại D suy ra AC là tiếp tuyến của đường tròn (B; BD). Chứng minh \(\widehat {BMH} = \widehat {BKH}\)dựa vào hai tam giác đồng dạng. Lời giải chi tiết
a) Ta có tam giác BEC vuông tại E nên nội tiếp đường tròn đường kính BC. (1) Tam giác BDC vuông tại D nên nội tiếp đường tròn đường kính BC. (2) Từ (1) và (2) suy ra bốn điểm B, C, D, E cùng thuộc đường tròn đường kính BC. b) Ta có BD là bán kính đường tròn (B; BD) và BD \( \bot \)AC nên AC là tiếp tuyến của đường tròn (B; BD). c) Ta có \(\Delta BHD\backsim \Delta BDC\)(g.g), suy ra BD2 = BH.BC. Ta lại có BD = BK (bán kính đường tròn (B;BD)) nên BK2 = BH.BC. Suy ra \(\Delta BHK\backsim \Delta BKC\)(c.g.c), do đó \(\widehat {BKH} = \widehat {BCK}\) Mà \(\widehat {BMH} = \widehat {BCK}\) (cùng phụ với \(\widehat {ABC}\)) nên\(\widehat {BMH} = \widehat {BKH}\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
