Bài 1.40 trang 21 SBT giải tích 12Giải bài 1.40 trang 21 sách bài tập giải tích 12. Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a>0). Quảng cáo
Đề bài Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số \(a\left( {a > 0} \right).\) Phương pháp giải - Xem chi tiết - Lập hàm số tính diện tích tam giác theo biến là một cạnh góc vuông. - Xét hàm tìm GTLN và kết luận. Lời giải chi tiết
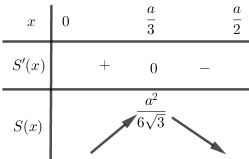
Xét tam giác ABC vuông tại A như hình vẽ. Gọi số đo cạnh góc vuông \(AB\) là \(x,0 < x < \dfrac{a}{2}\) (vì \(AB < BC\) \( \Rightarrow 2AB < AB + BC = a\) \( \Rightarrow AB < \frac{a}{2}\)) Khi đó, cạnh huyền \(BC = a-x\), cạnh góc vuông còn lại là: \(AC = \sqrt {B{C^2} - A{B^2}} \) \( = \sqrt {{{(a - x)}^2} - {x^2}} \) Hay \(AC = \sqrt {{a^2} - 2ax} \) Diện tích tam giác \(ABC\) là: \(S(x) = \dfrac{1}{2}x\sqrt {{a^2} - 2ax} \) \(S'(x) = \dfrac{1}{2}\sqrt {{a^2} - 2ax} - \dfrac{1}{2}\dfrac{{ax}}{{\sqrt {{a^2} - 2ax} }}\)\( = \dfrac{{a(a - 3x)}}{{2\sqrt {{a^2} - 2ax} }}\) \(S'(x) = 0 \Leftrightarrow x = \dfrac{a}{3}\) Bảng biến thiên:
Tam giác có diện tích lớn nhất khi \(AB = \dfrac{a}{3};BC = \dfrac{{2a}}{3}\). Loigiaihay.com
|





















Danh sách bình luận