Bài 14 trang 121 Vở bài tập toán 8 tập 2

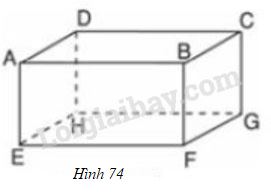
Đề bài

Cho hình hộp chữ nhật \(ABCD.EFGH\) (h.74):

a) Kể tên các đường thẳng song song với mp \((EFGH)\).

b) Đường thẳng \(AB\) song song với những mặt phẳng nào?

c) Đường thẳng \(AD\) song song với những đường thẳng nào?

Lời giải chi tiết

Các mặt của hình hộp chữ nhật đều là hình chữ nhật, do đó ra có:

- \(AB//EF\) mà \(EF \subset mp\left( {EFGH} \right)\), do đó \(AB//mp\left( {EFGH} \right)\)

- \(BC//GF\) mà \(GF \subset mp\left( {EFGH} \right)\), do đó \(BC//mp\left( {EFGH} \right)\)

- \(DC//GH\) mà \(GH \subset mp\left( {EFGH} \right)\), do đó \(DC//mp\left( {EFGH} \right)\)

- \(AD//EH\) mà \(EH \subset mp\left( {EFGH} \right)\), do đó \(AD//mp\left( {EFGH} \right)\)

Vậy các đường thẳng \(AB,BC,CD,DA\) đều song song với \(mp\left( {EFGH} \right)\).

b) \(AB//CD\) mà \(CD \subset mp\left( {CDHG} \right)\), do đó \(AB//mp(CDHG)\)

\(AB//EF\) mà \(EF \subset mp\left( {EFGH} \right)\), do đó \(AB//mp(EFGH)\)

Vậy \(AB\) song song với \(mp(CDHG)\) và \(mp(EFGH)\)

c) Trong \(mp(ABCD)\), \(AD//BC\) (1)

Trong \(mp(ADHE)\), \(AD//HE\) (2)

Trong \(mp(BCGF)\), \(GF//BC\) (3)

Từ (1),(3): \(AD//BC\) và \(GF//BC\), do đó \(AD//GF\).

Vậy \(AD\) song song với các đường thẳng \(BC,GF\) và \(EH\).

Loigiaihay.com