Bài 12 trang 119 Vở bài tập toán 8 tập 2

Đề bài

Một bể nước hình hộp chữ nhật có chiều dài \(2m\). Lúc đầu bể không có nước. Sau khi đổ vào bể \(120\) thùng nước, mỗi thùng chứa \(20\) lít thì mực nước của bể cao \(0,8m\).

a) Tính chiều rộng của bể nước.

b) Người ta đổ thêm vào bể \(60\) thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?

Lời giải chi tiết

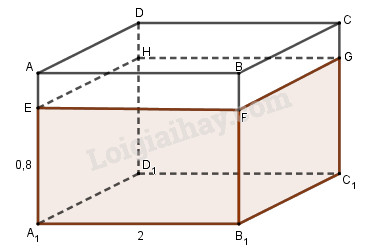
a) Giả sử bể nước là hình hộp chữ nhật \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có chiều dài là \(AB = {A_1}{B_1} = 2m\) (h.72).

Chú ý: \(1l = 1d{m^3} = \dfrac{1}{{1000}}{m^3}\).

Sau khi đổ vào bể \(120\) thùng nước, số nước đó được chứa đầy trong hình hộp chữ nhật \(EFGH.{A_1}{B_1}{C_1}{D_1}\) có chiều cao \(0,8m\).

Vậy ta có: \(V = E{A_1}.{A_1}{B_1}.{B_1}{C_1}\) \( = 120.20\left( {d{m^3}} \right)\) \( = 2,4\left( {{m^3}} \right)\)

\( \Rightarrow 0,8.2.{B_1}{C_1} = 2,4\left( {{m^3}} \right)\) \( \Rightarrow {B_1}{C_1} = \dfrac{{2,4}}{{0,8.2}} = 1,5\left( m \right)\)

b) Sau khi đổ thêm \(60\) thùng nước vào bể thì bể đầy, do đó thể tích bể là:

\(\left( {120 + 60} \right).20\left( {d{m^3}} \right) = 3,6{m^3}.\)

Vậy ta có: \(A{A_1}.{A_1}{B_1}.{B_1}{C_1}\) \( = A{A_1}.2.1,5 = 3,6\left( {{m^3}} \right)\)

Tính được: \(A{A_1} = 3,6:\left( {2.1,5} \right) = 1,2\left( m \right)\).

Loigiaihay.com