Bài 1.36 trang 21 SBT giải tích 12

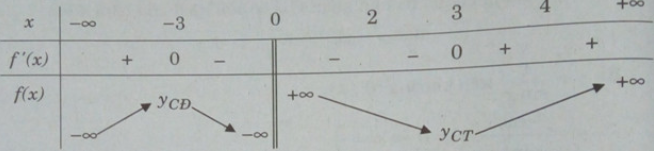
Đề bài

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x) = x + \dfrac{9}{x}\) trên đoạn \(\left[ {2;4} \right]\)

(Đề thi tốt nghiệp THPT năm 2008)

Lời giải chi tiết

Ta có: \(f'(x) = 1 - \dfrac{9}{{{x^2}}} = \dfrac{{{x^2} - 9}}{{{x^2}}}\)

\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3 \in \left[ {2;4} \right]\\x =  - 3 \notin \left[ {2;4} \right]\end{array} \right.\)

Mà \(f\left( 2 \right) = \dfrac{{13}}{2},f\left( 3 \right) = 6,f\left( 4 \right) = \dfrac{{25}}{4}\)

Suy ra : \(\mathop {\min }\limits_{{\rm{[}}2;4]} f(x) = 6;\mathop {\max }\limits_{{\rm{[}}2;4]} f(x) = \dfrac{{13}}{2}\).

Cách khác:

TXĐ: D = R\{0}

\(f'\left( x \right) = 1 - \frac{9}{{{x^2}}} = \frac{{{x^2} - 9}}{{{x^2}}}\)

f′(x) = 0 ⇔ x = 3 hoặc x = -3

Hàm số nghịch biến trong các khoảng (-3;0), (0;3) và đồng biến trong các khoảng (−∞;3), (3;+∞)

Bảng biến thiên:

Ta có: [2;4] ⊂ (0; +∞); f(2) = 6,5; f(3) = 6; f(4) = 6,25

Suy ra

min f(x) = f(3) = 6; max f(x) = f(2) = 6,5.

Loigiaihay.com