Bài 10 trang 148 Vở bài tập toán 8 tập 1

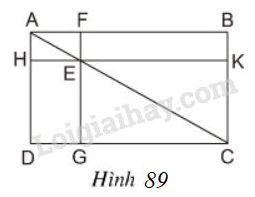
Đề bài

Cho hình \(89\), trong đó \(ABCD\) là hình chữ nhật, \(E\) là một điểm bất kì nằm trên đường chéo \(AC, FG // AD\), và \(HK // AB\).

Chứng minh rằng hai hình chữ nhật \(EFBK\) và \(EGDH\) có cùng diện tích. 

Lời giải chi tiết

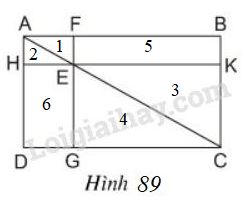
Trước hết, ta có nhận xét: Đường chéo của một hình chữ nhật chia hình đó thành hai tam giác vuông có diện tích bằng nhau.

Thật vậy, xét hình chữ nhật \(ABCD\). Ta có \(\Delta ABC =\Delta  CDA\,\,(c.c.c)\) nên \({S_{ABC}} = {S_{CDA\,}}\)

Ta kí hiệu diện tích các hình như trên hình \(90.\) 

Ta thấy \(AHEF\) và \(EGCK\) là các hình bình hành có một góc vuông nên là hình chữ nhật.

Với nhận xét trên, ta có

\({S_{ABC}} = {S_{CDA\,}}\,,\,\,{S_1} = {S_2},\,\,{S_3} = {S_4}\)

Suy ra \({S_{ABC}} - {S_1} - {S_3} = {S_{CDA\,}} - {S_2} - {S_4}\)

tức là \({S_5} = {S_6}\)

Vậy hai hình chữ nhật \(EFBK\) và \(EGDH\) có cùng diện tích.

Loigiaihay.com