Đề thi giữa kì 2 Toán 9 - Đề số 4Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 6. Mỗi câu hỏi thí sinh chỉ chọn một phương án.Đề bài
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 6. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho hàm số \(y = {x^2}\). Với \(y = 4\) thì giá trị của \(x\) bằng
Câu 2 :
Cho phương trình \({x^2} - 2x - m + 1 = 0\) có nghiệm \({x_1} = - 1\). Giá trị của tham số m là:
Câu 3 :
Biết rằng \({x^2} - 5x + 2 = 0\) có hai nghiệm \({x_1};{x_2}\). Khi đó \({x_1}^2 + {x_2}^2\) bằng
Câu 4 :
Cho bảng tần số - tần số tương đối điểm kiểm tra của lớp 9B như sau:
Tần số tương đối của điểm 8 là bao nhiêu?
Câu 5 :
Tính bán kính đường tròn nội tiếp của tam giác đều có cạnh bằng 16cm.
Câu 6 :
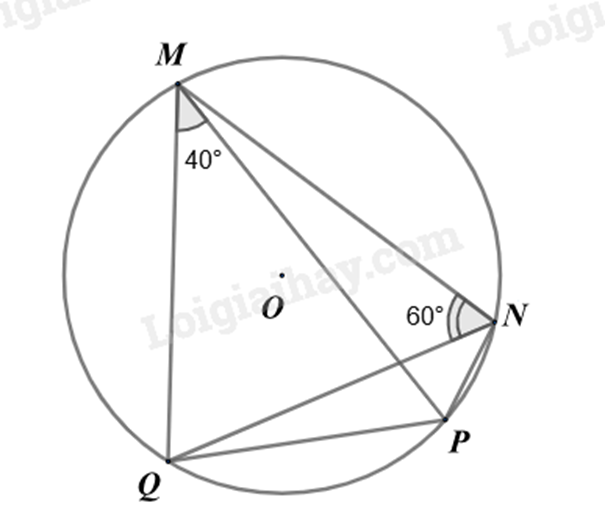
Cho tứ giác \(MNPQ\) nội tiếp đường tròn (O). Biết \(\widehat {MNQ} = 60^\circ ,\widehat {QMP} = 40^\circ \). Số đo góc MQP là
Phần II. Câu hỏi trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Tại một hội nghị khoa học quốc tế năm 2022, ban tổ chức khảo sát số lượng ngôn ngữ mà mỗi đại biểu có thể sử dụng. Kết quả thu được như sau:
a) Bảng tần số tương đối cho dữ liệu trên như sau:
Đúng
Sai
b) Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là 35%.
Đúng
Sai
c) Biểu đồ tần số tương đối cho dữ liệu trên là:
Đúng
Sai
d) Tại hội nghị khoa học quốc tế được tổ chức năm 2023, có 65 trong tổng số 180 đại biểu tham dự có thể sử dụng được từ 3 ngoại ngữ trở lên. Do đó tỉ lệ đại biểu sử dụng được từ 3 ngoại ngữ trở lên năm 2023 tăng so với năm 2022.
Đúng
Sai
Câu 2 :
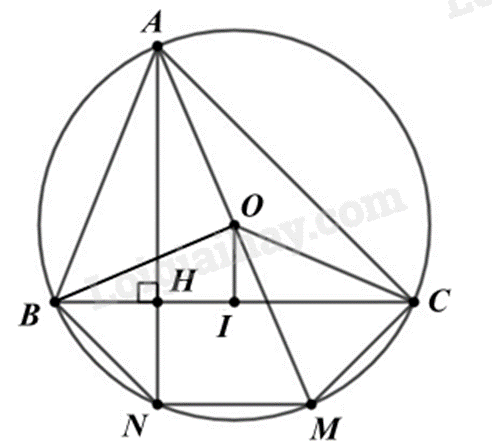
Cho tam giác ABC nhọn nội tiếp đường tròn tâm \(\left( O \right)\), đường cao AH, đường kính AM. Gọi I là trung điểm BC. a) \(\widehat {ACM} = 45^\circ \).
Đúng
Sai
b) \(\widehat {OAC} = \widehat {BAH}\).
Đúng
Sai
c) \(OI{\mkern 1mu} {\rm{//}}{\mkern 1mu} AH\).
Đúng
Sai
d) Gọi N là giao điểm của AH với đường tròn \(\left( O \right)\). Tứ giác BCMN là hình bình hành.
Đúng
Sai
Phần III. Câu hỏi trắc nghiệm trả lời ngắn
Thí sinh trả lời câu hỏi từ câu 1 đến câu 4
Câu 1 :
Cho hàm số \(y = \left( {2m + 2} \right){x^2}\). Tìm m để đồ thị hàm số đi qua điểm \(A\left( {x;y} \right)\) với \(\left( {x;y} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x - y = 2\end{array} \right.\). Đáp án:
Câu 2 :
Tích các giá trị của m để phương trình \(7m{x^2} - 24x - 4{m^2} = 0\) có nghiệm \(x = 2\). Đáp án:
Câu 3 :
Một phường cho trẻ em từ 2 tháng tuổi trở lên tiêm vắc xin 6 in 1. Bảng sau thống kê số mũi vắc xin 6 in 1 mà 60 trẻ em từ 2 tháng tuối đến 24 tháng tuổi của phường này đã tiêm. Trẻ em từ 2 tháng tuổi đến 24 tháng tuổi cần hoàn thành 4 mũi tiêm của vắc xin 6 in 1. Hỏi có bao nhiêu trẻ em của phường trên cần phải hoàn thành lộ trình tiêm vắc xin này? Đáp án:
Câu 4 :
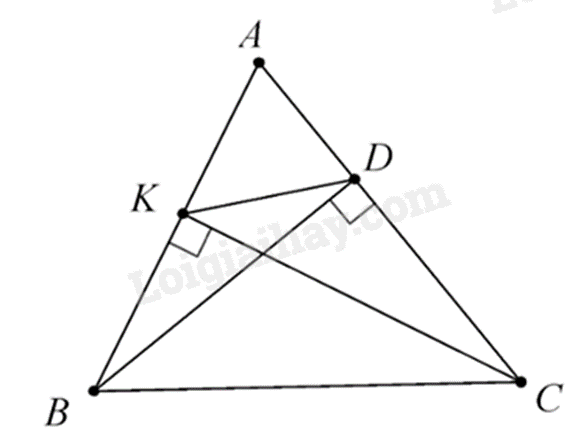
Cho tam giác ABC có CK và BD là hai đường cao. Biết \(\widehat {ACB} = 50^\circ \), số đo \(\widehat {AKD}\) bằng … (không cần ghi độ) Đáp án:
Phần IV. Tự luận
Lời giải và đáp án
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 6. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho hàm số \(y = {x^2}\). Với \(y = 4\) thì giá trị của \(x\) bằng
Đáp án : C Phương pháp giải :
Thay \(y = 4\) vào hàm số, ta tính được giá trị của \(x\) tương ứng. Lời giải chi tiết :
Thay \(y = 4\) vào hàm số \(y = {x^2}\) ta được \(4 = {x^2}\) suy ra \(x = 2\) hoặc \(x = - 2\) Vậy \(x = 2\) và \(x = - 2\). Đáp án C
Câu 2 :
Cho phương trình \({x^2} - 2x - m + 1 = 0\) có nghiệm \({x_1} = - 1\). Giá trị của tham số m là:
Đáp án : A Phương pháp giải :
Thay nghiệm \({x_1}\) vào phương trình để tìm m. Lời giải chi tiết :
Thay \({x_1} = - 1\) vào phương trình \({x^2} - 2x - m + 1 = 0\), ta được: \(\begin{array}{l}{\left( { - 1} \right)^2} - 2.\left( { - 1} \right) - m + 1 = 0\\1 + 2 - m + 1 = 0\\m = 4\end{array}\) Vậy m = 4. Đáp án A
Câu 3 :
Biết rằng \({x^2} - 5x + 2 = 0\) có hai nghiệm \({x_1};{x_2}\). Khi đó \({x_1}^2 + {x_2}^2\) bằng
Đáp án : B Phương pháp giải :
- Kiểm tra số nghiệm của phương trình \(a{x^2} + bx + c = 0\) bằng \(\Delta \): \(\Delta = {b^2} - 4ac\). - Sử dụng định lí Viète để tìm \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right.\). - Biến đổi \({x_1}^2 + {x_2}^2\) theo \({x_1} + {x_2};{x_1}{x_2}\). Lời giải chi tiết :
Ta có: \(\Delta = {\left( { - 5} \right)^2} - 4.2 = 17 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1};{x_2}\). Theo định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}{x_2} = 2\end{array} \right.\) \(\begin{array}{l}{x_1}^2 + {x_2}^2\\ = \left( {{x_1}^2 + 2{x_1}{x_2} + {x_2}^2} \right) - 2{x_1}{x_2}\\ = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\\ = {5^2} - 2.2\\ = 25 - 4\\ = 21\end{array}\) Đáp án B
Câu 4 :
Cho bảng tần số - tần số tương đối điểm kiểm tra của lớp 9B như sau:
Tần số tương đối của điểm 8 là bao nhiêu?
Đáp án : D Phương pháp giải :
Quan sát bảng tần số - tần số tương đối để xác định tần số tương đối của điểm 8. Lời giải chi tiết :
Tần số tương đối của điểm 8 là 17,5%. Đáp án D
Câu 5 :
Tính bán kính đường tròn nội tiếp của tam giác đều có cạnh bằng 16cm.
Đáp án : C Phương pháp giải :
Sử dụng công thức tính bán kính đường tròn nội tiếp tam giác đều cạnh a: \(r = \frac{{\sqrt 3 }}{6}a\). Lời giải chi tiết :
Bán kính đường tròn nội tiếp của tam giác đều cạnh bằng 16cm là: \(r = \frac{{\sqrt 3 }}{6} \cdot 16 = \frac{{8\sqrt 3 }}{3}\)cm Đáp án C
Câu 6 :
Cho tứ giác \(MNPQ\) nội tiếp đường tròn (O). Biết \(\widehat {MNQ} = 60^\circ ,\widehat {QMP} = 40^\circ \). Số đo góc MQP là
Đáp án : C Phương pháp giải :
Dựa vào hai góc nội tiếp cùng chắn một cung để tính \(\widehat {QNP}\), suy ra \(\widehat {MNP}\). Từ định lí tổng hai góc đối của tứ giác nội tiếp, tính \(\widehat {MQP}\). Lời giải chi tiết :
Vì tứ giác MNPQ nội tiếp đường tròn (O) nên \(\widehat {QMP} = \widehat {QNP}\) (hai góc nội tiếp chắn cung PQ), suy ra \(\widehat {QNP} = 40^\circ \). Ta có: \(\widehat {MNP} = \widehat {MPQ} + \widehat {QNP} = 60^\circ + 40^\circ = 100^\circ \). Áp dụng định lí tổng hai góc đối của tứ giác nội tiếp, ta có: \(\widehat {MQP} + \widehat {MNP} = 180^\circ \) Suy ra \(\widehat {MQP} = 180^\circ - \widehat {MNP} = 180^\circ - 100^\circ = 80^\circ \). Đáp án C
Phần II. Câu hỏi trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Tại một hội nghị khoa học quốc tế năm 2022, ban tổ chức khảo sát số lượng ngôn ngữ mà mỗi đại biểu có thể sử dụng. Kết quả thu được như sau:
a) Bảng tần số tương đối cho dữ liệu trên như sau:
Đúng
Sai
b) Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là 35%.
Đúng
Sai
c) Biểu đồ tần số tương đối cho dữ liệu trên là:
Đúng
Sai
d) Tại hội nghị khoa học quốc tế được tổ chức năm 2023, có 65 trong tổng số 180 đại biểu tham dự có thể sử dụng được từ 3 ngoại ngữ trở lên. Do đó tỉ lệ đại biểu sử dụng được từ 3 ngoại ngữ trở lên năm 2023 tăng so với năm 2022.
Đúng
Sai
Đáp án
a) Bảng tần số tương đối cho dữ liệu trên như sau:
Đúng
Sai
b) Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là 35%.
Đúng
Sai
c) Biểu đồ tần số tương đối cho dữ liệu trên là:
Đúng
Sai
d) Tại hội nghị khoa học quốc tế được tổ chức năm 2023, có 65 trong tổng số 180 đại biểu tham dự có thể sử dụng được từ 3 ngoại ngữ trở lên. Do đó tỉ lệ đại biểu sử dụng được từ 3 ngoại ngữ trở lên năm 2023 tăng so với năm 2022.
Đúng
Sai
Phương pháp giải :
a) Sử dụng công thức tính tần số tương đối cho dữ liệu: \(f = \frac{m}{N}.100\% \), trong đó m là tần số của giá trị và N là cỡ mẫu. Sau đó lập bảng tần số tương đối. b) Tính tổng tần số tương đối của các đại biểu sử dụng được ít nhất 2 ngoại ngữ. c) Từ bảng tần số tương đối đã lập để vẽ biểu đồ tần số tương đối phù hợp. Công thức đổi từ tần số tương đối sang độ: \(360^\circ .{f_i}\). d) Tính tần số tương đối của số đại biểu sử dụng được từ 3 ngoại ngữ trở nên trong năm 2022 và 2023. So sánh hai tần số tương đối với của số đại biểu sử dụng được từ 3 ngoại ngữ trong hai năm với nhau. Lời giải chi tiết :
a) Sai Tổng số đại biểu là: \(72 + 58 + 34 + 20 + 16 = 200\) Tần số tương đối của các giá trị 1; 2; 3; 4; \( \ge \)5 lần lượt là: \(\begin{array}{l}\frac{{72}}{{200}}.100\% = 36\% ;\frac{{58}}{{200}}.100\% = 29\% ;\frac{{34}}{{200}}.100\% = 17\% ;\\\frac{{20}}{{200}}.100\% = 10\% ;\frac{{16}}{{200}}.100\% = 8\% \end{array}\) Vậy bảng tần số tương đối cho dữ liệu trên như sau:
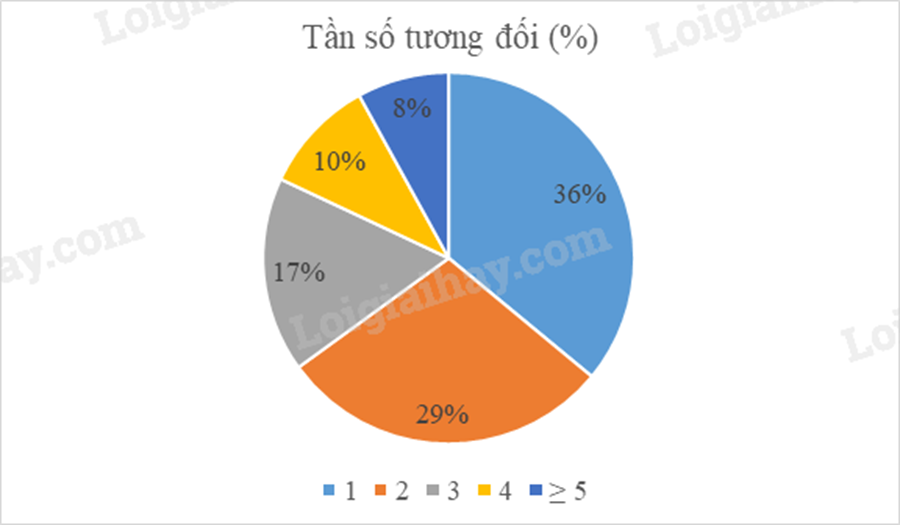
b) Sai Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là: \(29 + 17 + 10 + 8 = 64\left( \% \right)\). c) Đúng Từ bảng tần số tương đối, ta có số độ tương ứng với các giá trị tần số là: \(\begin{array}{l}360^\circ .36\% \approx 130^\circ ;360^\circ .29\% \approx 104^\circ ;360^\circ .17\% \approx 61^\circ ;\\360^\circ .10\% = 36^\circ ;360^\circ .8\% = 29^\circ \end{array}\) Vẽ được biểu đồ tần số tương đối:
d) Đúng Tỉ lệ đại biểu sử dụng từ 3 ngôn ngữ trở lên trong hội nghị năm 2022 là: \(17\% + 10\% + 8\% = 35\% \) Tỉ lệ đại biểu sử dụng từ 3 ngôn ngữ trở lên trong hội nghị năm 2023 là: \(\frac{{65}}{{180}}.100\% \approx 36,1\% \) Ta thấy 36,1% > 35% nên tỉ lệ đại biểu sử dụng được từ 3 ngoại ngữ trở lên năm 2023 tăng so với năm 2022. Đáp án: SSĐĐ
Câu 2 :
Cho tam giác ABC nhọn nội tiếp đường tròn tâm \(\left( O \right)\), đường cao AH, đường kính AM. Gọi I là trung điểm BC. a) \(\widehat {ACM} = 45^\circ \).
Đúng
Sai
b) \(\widehat {OAC} = \widehat {BAH}\).
Đúng
Sai
c) \(OI{\mkern 1mu} {\rm{//}}{\mkern 1mu} AH\).
Đúng
Sai
d) Gọi N là giao điểm của AH với đường tròn \(\left( O \right)\). Tứ giác BCMN là hình bình hành.
Đúng
Sai
Đáp án
a) \(\widehat {ACM} = 45^\circ \).
Đúng
Sai
b) \(\widehat {OAC} = \widehat {BAH}\).
Đúng
Sai
c) \(OI{\mkern 1mu} {\rm{//}}{\mkern 1mu} AH\).
Đúng
Sai
d) Gọi N là giao điểm của AH với đường tròn \(\left( O \right)\). Tứ giác BCMN là hình bình hành.
Đúng
Sai
Phương pháp giải :
a) Sử dụng hai góc nội tiếp chắn nửa đường tròn bằng \(90^\circ \). b) Sử dụng hai góc nội tiếp chắn cùng một cung thì bằng nhau để chứng minh \(\widehat {ABC} = \widehat {AMC}\). Kết hợp với tổng hai góc phụ nhau để suy ra \(\widehat {OAC} = \widehat {BAH}\). c) Chứng minh OI là đường cao nên \(OI \bot BC\), mà \(AH \bot BC\) nên \(AH//OI\). d) Sử dụng hai góc nội tiếp chắn nửa đường tròn bằng \(90^\circ \). Chứng minh MN // BC suy ra BCMN là hình thang. Chứng minh hai góc ở đáy \(\widehat {CBN} = \widehat {BCM}\) thông qua hai cung trên cùng một đường tròn gọi là bằng nhau nếu chúng có cùng số đo, suy ra BCMN là hình thang cân. Lời giải chi tiết :
a) Sai Vì \(\widehat {ACM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACM} = 90^\circ \). b) Đúng Xét (O) có: \(\widehat {ABC} = \widehat {AMC}\) (hai góc nội tiếp cùng chắn cung AC). Mà \(\widehat {BAH} + \widehat {ABC} = 90^\circ \left( {AH \bot BC} \right)\) Lại có: \(\widehat {OAC} + \widehat {AMC} = 90^\circ \) (tam giác ACM có \(\widehat {ACM} = 90^\circ \)). Suy ra \(\widehat {BAH} + \widehat {ABC} = \widehat {OAC} + \widehat {AMC}\) nên \(\widehat {BAH} = \widehat {OAC}\) c) Đúng Tam giác BOC cân tại O (OB = OC = R) có I là trung điểm của BC nên OI là đường trung tuyến đồng thời là đường cao. Suy ra \(OI \bot BC\) Mà \(AH \bot BC\) nên \(OI//AH\). d) Sai Xét (O) có \(\widehat {ANM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ANM} = 90^\circ \) suy ra \(AN \bot NM\) Mà \(BC \bot AN\) suy ra \(MN//BC\). Do đó tứ giác BCMN là hình thang. (1) Ta lại có: \(\widehat {BAN} = \widehat {CAM}\) (vì \(\widehat {BAH} = \widehat {OAC}\)) Do đó: $\overset\frown{BN}=\overset\frown{CM}$ $\overset\frown{BN}+\overset\frown{MN}=\overset\frown{CM}+\overset\frown{MN}$ $\overset\frown{BNM}=\overset\frown{CMN}$ Do đó \(\widehat {BCM} = \widehat {CBN}\) (2) Từ (1) và (2) suy ra tứ giác BCMN là hình thang cân. Đáp án: SĐĐS
Phần III. Câu hỏi trắc nghiệm trả lời ngắn
Thí sinh trả lời câu hỏi từ câu 1 đến câu 4
Câu 1 :
Cho hàm số \(y = \left( {2m + 2} \right){x^2}\). Tìm m để đồ thị hàm số đi qua điểm \(A\left( {x;y} \right)\) với \(\left( {x;y} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x - y = 2\end{array} \right.\). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Xác định tọa độ điểm \(A\left( {x;y} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x - y = 2\end{array} \right.\). (có thể sử dụng máy tính cầm tay đối với câu dạng trắc nghiệm) Khi đó thay tọa độ điểm A vào hàm số \(y = a{x^2}\) thì \({y_A} = a{x_A}^2\) nên \(a = \frac{{{y_A}}}{{{x_A}^2}}\) với \({x_A} \ne 0\). Lời giải chi tiết :
Ta tính được nghiệm của hê phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x - y = 2\end{array} \right.\) là \(\left( { - 1; - 4} \right)\). Khi đó điểm \(A\left( { - 1; - 4} \right)\) thuộc đồ thị hàm số \(y = \left( {2m + 2} \right){x^2}\). Thay \(x = - 1;y = - 4\) vào \(y = \left( {2m + 2} \right){x^2}\), ta được: \(\begin{array}{l} - 4 = \left( {2m + 2} \right).{\left( { - 1} \right)^2}\\2m + 2 = \frac{{ - 4}}{{{{\left( { - 1} \right)}^2}}}\\2m + 2 = - 4\\2m = - 6\\m = - 3\end{array}\) Đáp án: -3
Câu 2 :
Tích các giá trị của m để phương trình \(7m{x^2} - 24x - 4{m^2} = 0\) có nghiệm \(x = 2\). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Thay \(x = 2\) vào phương trình để tìm m. Đưa phương trình về phương trình tích, sử dụng công thức nghiệm hoặc sử dụng máy tính cầm tay để tìm m. Lời giải chi tiết :
Thay \(x = 2\) vào phương trình \(7m{x^2} - 24x - 4{m^2} = 0\), ta được: \(\begin{array}{l}7m{x^2} - 24x - 4{m^2} = 0\\7m{.2^2} - 24.2 - 4{m^2} = 0\\28m - 48 - 4{m^2} = 0\\4{m^2} - 28m + 48 = 0\\{m^2} - 7m + 12 = 0\end{array}\) Suy ra \({m_1} = 4;{m_2} = 3\) Vậy tích các giá trị của m là: \(4.3 = 12\). Đáp án: 12
Câu 3 :
Một phường cho trẻ em từ 2 tháng tuổi trở lên tiêm vắc xin 6 in 1. Bảng sau thống kê số mũi vắc xin 6 in 1 mà 60 trẻ em từ 2 tháng tuối đến 24 tháng tuổi của phường này đã tiêm. Trẻ em từ 2 tháng tuổi đến 24 tháng tuổi cần hoàn thành 4 mũi tiêm của vắc xin 6 in 1. Hỏi có bao nhiêu trẻ em của phường trên cần phải hoàn thành lộ trình tiêm vắc xin này? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Xác định tổng số trẻ em chưa hoàn thành lộ trình tiêm vắc xin dựa vào bảng tần số. Số trẻ em chưa hoàn thành lộ trình tiêm có số mũi tiêm nhỏ hơn 4. Lời giải chi tiết :
Vì trẻ em từ 2 tháng tuổi đến 24 tháng tuổi cần hoàn thành 4 mũi tiêm của vắc xin 6 in 1 nên số trẻ em của phường cần phải hoàn thành lộ trình tiêm vắc xin là: \(7 + 8 + 18 + 15 = 48\) (trẻ em) Đáp án: 48
Câu 4 :
Cho tam giác ABC có CK và BD là hai đường cao. Biết \(\widehat {ACB} = 50^\circ \), số đo \(\widehat {AKD}\) bằng … (không cần ghi độ) Đáp án: Đáp án
Đáp án: Phương pháp giải :
Chứng minh tứ giác BKDC là tứ giác nội tiếp, suy ra hai góc đối có tổng bằng \(180^\circ \). Kết hợp với hai góc kề bù có tổng bằng \(180^\circ \). Lời giải chi tiết :
Xét tam giác BKC và tam giác BDC có \(\widehat {BKC} = \widehat {BDC} = 90^\circ \) tam giác BKC và tam giác BDC nội tiếp đường tròn đường kính BC. Do đó \(B,K,D,C\) thuộc đường tròn đường kính BC hay tứ giác BKDC nội tiếp đường tròn đường kính BC. Suy ra \(\widehat {BKD} + \widehat {BCD} = 180^\circ \) (định lí tổng hai góc đối của tứ giác nội tiếp) Mà \(\widehat {BKD} + \widehat {AKD} = 180^\circ \) (hai góc kề bù) Do đó \(\widehat {BCD} = \widehat {AKD}\) (cùng bù với \(\widehat {BKD}\)) Mà \(\widehat {BCD} = \widehat {BCA} = 50^\circ \) nên \(\widehat {AKD} = 50^\circ \). Đáp án: 50
Phần IV. Tự luận
Phương pháp giải :
Gọi vận tốc của xe máy là \(x\left( {{\rm{km/h}}} \right)\left( {x > 0} \right)\) Biểu diễn vận tốc, thời gian xe máy, ô tô đi hết quãng đường. Lập phương trình dựa vào đề bài. Giải phương trình, kết hợp điều kiện ban đầu của \(x\). Lời giải chi tiết :
Gọi vận tốc của xe máy là \(x\left( {{\rm{km/h}}} \right)\left( {x > 0} \right)\) Vận tốc của ô tô là \(x + 24\left( {{\rm{km/h}}} \right)\) Thời gian xe máy đi hết quãng đường là: \(\frac{{120}}{x}\)(h) Thời gian ô tô đi hết quãng đường là: \(\frac{{120}}{{x + 24}}\)(h) Đổi 30 phút = \(\frac{1}{2}\)(h); 20 phút = \(\frac{1}{3}\)(h) Theo đề bài ta có phương trình: \(\begin{array}{l}\frac{{120}}{{x + 24}} + \frac{1}{3} = \frac{{120}}{x} - \frac{1}{2}\\\frac{{120x.3.2}}{{6x\left( {x + 24} \right)}} + \frac{{\left( {x + 24} \right).x.2}}{{6x\left( {x + 24} \right)}} = \frac{{120\left( {x + 24} \right).3.2}}{{6x\left( {x + 24} \right)}} - \frac{{\left( {x + 24} \right).3.x}}{{6x\left( {x + 24} \right)}}\\720x + 2{x^2} + 48x = 720x + 17280 - 3{x^2} - 72x\\5{x^2} + 120x - 17280 = 0\end{array}\) Giải phương trình, ta được: \({x_1} = 48\left( {t/m} \right);{x_2} = - 72\left( L \right)\) Vậy vận tốc xe máy là \(48\left( {{\rm{km/h}}} \right)\). Phương pháp giải :
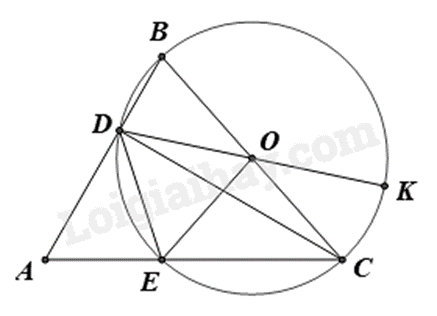
a) Từ góc nội tiếp chắn nửa đường tròn để chứng minh tam giác ADC vuông tại D. Kết hợp với \(\widehat {BAC} = 60^\circ \) suy ra góc \(\widehat {ECD}\) chắn cung DE. b) Chứng minh tam giác ODE cân tại O có \(\widehat {DOE} = 60^\circ \) nên tam giác ODE đều. Suy ra số đo góc EDK Lời giải chi tiết :
a) Ta có: \(\widehat {BDC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta BDC\) vuông tại D. Mà \(\widehat A = 60^\circ \) (gt) suy ra \(\widehat {ACD} = 90^\circ - 60^\circ = 30^\circ \) hay \(\widehat {ECD} = 30^\circ \). Xét đường tròn (O) có \(\widehat {ECD}\) là góc nội tiếp chắn cung DE nên sđ$\overset\frown{DE}=2.\widehat{ECD}=2.30{}^\circ =60{}^\circ $. b) Vì OD = OE (bán kính đường tròn) nên \(\Delta ODE\) cân tại O. Mà \(\widehat {DOE} = \)sđ$\overset\frown{DE}$\( = 60^\circ \) (góc ở tâm chắn cung DE) Suy ra \(\Delta ODE\) đều. Do đó \(\widehat {EDO} = 60^\circ \) hay \(\widehat {EDK} = 60^\circ \). Phương pháp giải :
Sử dụng công thức nghiệm \(\Delta = {b^2} - 4ac\), tìm điều kiện của m để \(\Delta \ge 0\) Sử dụng định lí Viète để tìm \({x_2}\): \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a}\\{x_1}.{x_2} = \frac{c}{a}\end{array} \right.\) Thay \({x_1};{x_2}\) vào P để tìm giá trị nhỏ nhất của P. Lời giải chi tiết :
Ta có: \(\Delta = {\left( { - 2} \right)^2} - 4.\left( {m - 3} \right) = 4 - 4m + 12 = - 4m + 16\) Để phương trình có hai nghiệm thì \(\Delta \ge 0\) hay \( - 4m + 16 \ge 0\), suy ra \(m \le 4\). Theo định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - \left( { - 2} \right)}}{1} = 2\\{x_1}.{x_2} = \frac{{m - 3}}{1} = m - 3\end{array} \right.\). Ta có: \(\begin{array}{l}P = {x_1}^2 + {x_2}^2 + {\left( {{x_1}{x_2}} \right)^2}\\ = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + {\left( {{x_1}{x_2}} \right)^2}\\ = {2^2} - 2\left( {m - 3} \right) + {\left( {m - 3} \right)^2}\\ = 4 - 2m + 6 + {m^2} - 6m + 9\\ = {m^2} - 8m + 19\\ = {m^2} - 8m + 16 + 3\end{array}\) \( = {\left( {m - 4} \right)^2} + 3 \ge 3\) với mọi \(m\). Dấu “=” xảy ra là giá trị nhỏ nhất của biểu thức. Suy ra giá trị nhỏ nhất của P bằng 3 khi \(m - 4 = 0\) hay \(m = 4\). Vậy \(m = 4\) thì P đạt giá trị nhỏ nhất.
|




























Danh sách bình luận