Đề thi giữa kì 1 Toán 9 - Đề số 4Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.Đề bài
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho phương trình \(12x - 5y = 4\). Hệ số a, b, c lần lượt là:
Câu 3 :
Tổng các nghiệm của phương trình \(\left( {2x + 5} \right)\left( {x - 3} \right) = 0\) là:
Câu 4 :
Nghiệm của phương trình \(\frac{{x + 2}}{{x - 4}} - 1 = \frac{{30}}{{\left( {x + 3} \right)\left( {x - 4} \right)}}\) là:
Câu 5 :
Bất đẳng thức \(n \le 5\) có thể được phát biểu là
Câu 6 :
Cho các số thực \(x,y,z\) thỏa mãn \(x < y\). Khẳng định nào sau đây là sai:
Câu 7 :
Hệ thức nào sau đây là bất đẳng thức?
Câu 8 :
Bất phương trình \(2x - 1 \le x + 4\) có nghiệm là
Câu 9 :
Cho tam giác ABC vuông tại A có AB = 8cm, AC = 6cm. Tính tỉ số lượng giác tanC?
Câu 10 :
Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là đúng?
Câu 11 :
Giá trị của biểu thức \(A = \tan 45^\circ .\sin 60^\circ .\cot 30^\circ \) là
Câu 12 :
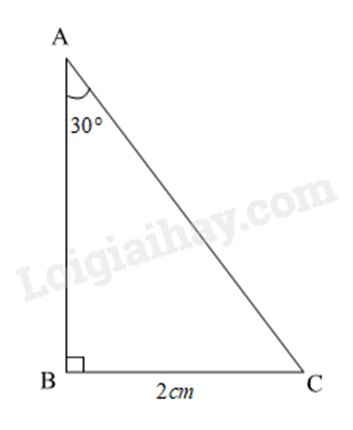
Cho tam giác ABC vuông tại B có \(\widehat A = 30^\circ ,BC = 2cm\). Độ dài cạnh AB là:
Phần II. Câu hỏi trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Một đội xe dự định dùng \(x\) xe cùng loại để chở 120 tấn hàng ủng hộ người dân vùng lũ. Lúc sắp khởi hành đội được bổ sung thêm \(\frac{1}{3}\) lượng xe ban đầu, nhờ vậy so với ban đầu mỗi xe phải chở ít hơn 2 tấn. (Khối lượng hàng mỗi xe phải chở là như nhau) a) Thực tế mỗi xe phải chở \(\frac{{90}}{x}\) tấn hàng.
Đúng
Sai
b) \(\frac{{90}}{x} - \frac{{120}}{x} = 2\).
Đúng
Sai
c) Số xe thực tế là 15 xe.
Đúng
Sai
d) Thực tế mỗi xe chở 6 tấn hàng.
Đúng
Sai
Câu 2 :
Một trường THCS cần mua x quyển vở và y cây bút để làm phần thưởng cho học sinh Xuất sắc và học sinh Giỏi. Mỗi quyển vở có giá niêm yết là 8 000 đồng, mỗi cây bút có giá niêm yết 6 000 đồng nên số tiền nhà trường cần chi trả là 11 triệu 200 nghìn đồng. Vì mua với số lượng lớn nên đại lý bán quyết định giảm giá 5% cho mỗi quyển vở và 6% cho mỗi cây bút, vì thế nhà trường chỉ cần trả 10 triệu 604 nghìn đồng. Biết 40% học sinh của trường là học sinh Xuất sắc và học sinh Giỏi, mỗi học sinh Xuất sắc được thưởng 5 quyển vở và 3 cây bút; mỗi học sinh Giỏi được thưởng 3 quyển vở và 2 cây bút. a) \(8\,000x + 6\,000y = 11\,200\,000\)
Đúng
Sai
b) \(7\,520x + 5\,700y = 10\,564\,000\)
Đúng
Sai
c) \(x = 950;y = 600\)
Đúng
Sai
d) Tổng số học sinh của trường là 600 học sinh.
Đúng
Sai
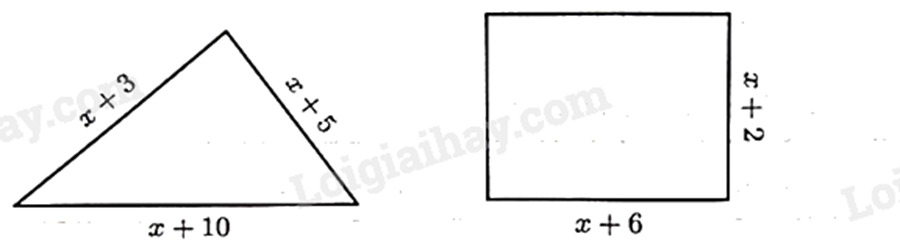
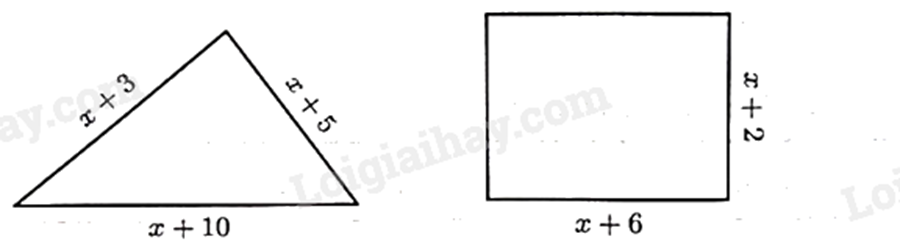
a) Chu vi hình tam giác và hình chữ nhật lần lượt là \(3x + 18\) và \(4x + 16\).
Đúng
Sai
b) \(4x + 16 > 3x + 18\).
Đúng
Sai
c) \(x < 2\)
Đúng
Sai
d) Với x = 1 thì chu vi tam giác bằng diện tích hình chữ nhật.
Đúng
Sai
Câu 4 :
Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = 12cm, BC = 20cm. Vẽ AD là đường phân giác của góc BAC. a) Độ dài BH là 7,2cm.
Đúng
Sai
b) \(\sin DAC = \frac{{\sqrt 2 }}{2}\).
Đúng
Sai
c) \(\tan HAD \approx 7,12\).
Đúng
Sai
d) \(AH = BC.\sin B.\cos B\).
Đúng
Sai
Phần III. Câu hỏi trắc nghiệm trả lời ngắn
Thí sinh trả lời câu hỏi từ câu 1 đến câu 6
Câu 1 :
Phương trình \({\left( {x - 3} \right)^2} - 4{x^2} = 0\) có hai nghiệm \({x_1};{x_2}\) \(\left( {{x_1} < {x_2}} \right)\). Tính giá trị của biểu thức \({x_1} + 3{x_2}\). Đáp án:
Câu 2 :
Nghiệm \({x_0}\) của phương trình \(\frac{1}{{x - 2}} - \frac{2}{{x - 1}} = \frac{5}{{\left( {x - 2} \right)\left( {x - 1} \right)}}\) thỏa mãn biểu thức \(S = {x_0}^3 + 2{x_0}^2 + 2024\). Tính giá trị của S. Đáp án:
Câu 3 :
Hệ phương trình \(\left\{ \begin{array}{l}2\left( {x - 2y} \right) + 3\left( {x + 2y} \right) = 4\\\left( {x - y} \right) + 2\left( {x + y} \right) = 1\end{array} \right.\) có cặp nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\). Tính giá trị của biểu thức \(A = - 25{x_0} - 7{y_0}\). Đáp án:
Câu 4 :
Bạn An đăng ký tham gia khóa học tiếng Anh ở một trung tâm ngoại ngữ. Qua hai bài kiểm tra của khoá học, bạn An đã đạt lần lượt 62 và 67 điểm (thang điểm 100). Bạn phấn đấu đạt điểm trung bình ít nhất là 70 sau ba lần kiểm tra. Để có kết quà này, ở lần kiểm tra thứ ba, bạn An phải được ít nhất bao nhiêu điểm? (số điểm đạt được là các số tự nhiên). Đáp án:
Câu 5 :
Hải đăng Trường Sa Lớn nằm trên đảo Trường Sa Lớn - “thủ phủ” quần đảo Trường Sa - có chiều cao bao nhiêu? Biết rằng tia nắng mặt trời chiếu qua đỉnh của ngọn hải đăng hợp với mặt đất 1 góc 35 độ và bóng của ngọn hải đăng trên mặt đất dài 20m. (làm tròn đến hàng đơn vị)
Đáp án:
Câu 6 :
Cho góc nhọn \(\alpha \) thỏa mãn \(0^\circ < \alpha < 50^\circ \). Rút gọn biểu thức \(A = \sin \left( {\alpha + 40^\circ } \right) - \sin \left( {\alpha + 30^\circ } \right) - \cos \left( {50^\circ - \alpha } \right) + \cos \left( {60^\circ - \alpha } \right)\) về biểu thức chỉ chứa tỉ số lượng giác sin của một góc. Đáp án: Lời giải và đáp án
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Cho phương trình \(12x - 5y = 4\). Hệ số a, b, c lần lượt là:
Đáp án : D Phương pháp giải :
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\), trong đó a, b và c là các số đã biết (\(a \ne 0\) hoặc \(b \ne 0\)). Lời giải chi tiết :
Phương trình \(12x - 5y = 4\) có hệ số \(a = 12\), \(b = - 5\) và \(c = 4\). Đáp án D.
Đáp án : C Phương pháp giải :
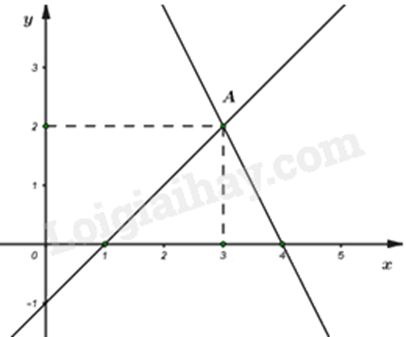
Xác định tọa độ của điểm A. Thay \({x_A};{y_A}\) vào các hệ phương trình xem hệ nào thỏa mãn. Lời giải chi tiết :
Quan sát hệ trục tọa độ, ta thấy tọa độ điểm A là \(A\left( {3;2} \right)\). Cặp số \(\left( {3;2} \right)\) là nghiệm của phương trình \(\left\{ \begin{array}{l}2x + y = 8\\x - y = 1\end{array} \right.\) vì \(\left\{ \begin{array}{l}2.3 + 2 = 8\\3 - 2 = 1\end{array} \right.\). Đáp án C.
Câu 3 :
Tổng các nghiệm của phương trình \(\left( {2x + 5} \right)\left( {x - 3} \right) = 0\) là:
Đáp án : B Phương pháp giải :
Giải phương trình tích và cộng tổng các nghiệm của phương trình. Lời giải chi tiết :
Ta có: \(\left( {2x + 5} \right)\left( {x - 3} \right) = 0\) \(2x + 5 = 0\) hoặc \(x - 3 = 0\) \(x = - \frac{5}{2}\) hoặc \(x = 3\). Tổng của hai nghiệm là: \( - \frac{5}{2} + 3 = \frac{1}{2}\). Đáp án B.
Câu 4 :
Nghiệm của phương trình \(\frac{{x + 2}}{{x - 4}} - 1 = \frac{{30}}{{\left( {x + 3} \right)\left( {x - 4} \right)}}\) là:
Đáp án : A Phương pháp giải :
Tìm điều kiện xác định của phương trình. Dựa vào cách giải phương trình chứa ẩn ở mẫu. Lời giải chi tiết :
ĐKXĐ: \(x - 4 \ne 0\) và \(x + 3 \ne 0\) hay \(x \ne 4\) và \(x \ne - 3\). Ta có: \(\frac{{x + 2}}{{x - 4}} - 1 = \frac{{30}}{{\left( {x + 3} \right)\left( {x - 4} \right)}}\) \(\frac{{\left( {x + 2} \right)\left( {x + 3} \right)}}{{\left( {x + 3} \right)\left( {x - 4} \right)}} - \frac{{\left( {x + 3} \right)\left( {x - 4} \right)}}{{\left( {x + 3} \right)\left( {x - 4} \right)}} = \frac{{30}}{{\left( {x + 3} \right)\left( {x - 4} \right)}}\) \(\left( {x + 2} \right)\left( {x + 3} \right) - \left( {x + 3} \right)\left( {x - 4} \right) = 30\) \(\begin{array}{l}{x^2} + 5x + 6 - \left( {{x^2} - x - 12} \right) = 30\\{x^2} + 5x + 6 - {x^2} + x + 12 = 30\\\left( {{x^2} - {x^2}} \right) + \left( {5x + x} \right) = 30 - 12 - 6\\6x = 12\\x = 2\left( {TM} \right)\end{array}\) Đáp án A.
Câu 5 :
Bất đẳng thức \(n \le 5\) có thể được phát biểu là
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về bất đẳng thức. Lời giải chi tiết :
Bất đẳng thức \(n \le 5\) có thể được phát biểu là n không lớn hơn 5. Đáp án D.
Câu 6 :
Cho các số thực \(x,y,z\) thỏa mãn \(x < y\). Khẳng định nào sau đây là sai:
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về tính chất của bất đẳng thức Lời giải chi tiết :
+ Với \(x < y\) thì \(x + z < y + z\) (cộng cả hai vế với \(z\)) nên A đúng. + Với \(x < y\) và \(z\) âm thì \(xz > yz\) nên B sai. + Với \(x < y\) thì \(x - z < y - z\) (cộng cả hai vế với \( - z\)) nên C đúng. + Với \(x < y\) và \(z\) dương thì \(xz < yz\) nên D đúng. Đáp án B.
Câu 7 :
Hệ thức nào sau đây là bất đẳng thức?
Đáp án : C Phương pháp giải :
Các hệ thức dạng \(a > b\) (hay \(a < b,a \ge b,a \le b\)) là bất đẳng thức và gọi a là vế tría, b là vế phải của bất đẳng thức. Lời giải chi tiết :
Trong các đáp án trên, chỉ có hệ thức \({y^2} \ge 0\) là bất đẳng thức. Đáp án C.
Câu 8 :
Bất phương trình \(2x - 1 \le x + 4\) có nghiệm là
Đáp án : A Phương pháp giải :
Dựa vào cách giải bất phương trình bậc nhất một ẩn để tìm nghiệm. Lời giải chi tiết :
Ta có: \(2x - 1 \le x + 4\) \(\begin{array}{l}2x - x \le 4 + 1\\x \le 5\end{array}\) Vậy bất phương trình \(2x - 1 \le x + 4\) có nghiệm là \(x \le 5\). Đáp án A.
Câu 9 :
Cho tam giác ABC vuông tại A có AB = 8cm, AC = 6cm. Tính tỉ số lượng giác tanC?
Đáp án : D Phương pháp giải :
Dựa vào kiến thức về tỉ số lượng giác trong tam giác vuông. Lời giải chi tiết :
Tam giác ABC vuông tại A nên tỉ số lượng giác \(\tan C = \frac{{AB}}{{AC}} = \frac{8}{6} = \frac{4}{3}\). Đáp án D.
Câu 10 :
Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là đúng?
Đáp án : C Phương pháp giải :
Dựa vào tính chất về tỉ số lượng giác của hai góc phụ nhau: \(\sin \alpha = \cos \left( {90^\circ - \alpha } \right),\tan \alpha = \cot \left( {90^\circ - \alpha } \right)\). Lời giải chi tiết :
Trong tam giác ABC vuông tại A thì \(\widehat B\) và \(\widehat C\) là hai góc phụ nhau. Ta có: \(\sin B = \cos C,\tan B = \cot C\). Dẫn đến \(\sin B - \cos C = 0\) và \(\tan B - \cot C = 0\) nên đáp án C đúng. Đáp án C.
Câu 11 :
Giá trị của biểu thức \(A = \tan 45^\circ .\sin 60^\circ .\cot 30^\circ \) là
Đáp án : D Phương pháp giải :
Sử dụng bảng giá trị lượng giác của các góc đặc biệt \(\left( {30^\circ ,45^\circ ,60^\circ } \right)\) hoặc sử dụng máy tính cầm tay.
Lời giải chi tiết :
Ta có: \(A = \tan 45^\circ .\sin 60^\circ .\cot 30^\circ \) \( = 1.\frac{{\sqrt 3 }}{2}.\sqrt 3 = \frac{3}{2}\) Đáp án D.
Câu 12 :
Cho tam giác ABC vuông tại B có \(\widehat A = 30^\circ ,BC = 2cm\). Độ dài cạnh AB là:
Đáp án : A Phương pháp giải :
Biểu diễn AB theo BC và tỉ số lượng giác của góc A. Lời giải chi tiết :
Ta có: \(\cot A = \frac{{AB}}{{BC}}\) suy ra \(AB = BC.\cot A = 2.\cot 30^\circ = 2.\sqrt 3 = 2\sqrt 3 \). Đáp án A.
Phần II. Câu hỏi trắc nghiệm đúng sai
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1 :
Một đội xe dự định dùng \(x\) xe cùng loại để chở 120 tấn hàng ủng hộ người dân vùng lũ. Lúc sắp khởi hành đội được bổ sung thêm \(\frac{1}{3}\) lượng xe ban đầu, nhờ vậy so với ban đầu mỗi xe phải chở ít hơn 2 tấn. (Khối lượng hàng mỗi xe phải chở là như nhau) a) Thực tế mỗi xe phải chở \(\frac{{90}}{x}\) tấn hàng.
Đúng
Sai
b) \(\frac{{90}}{x} - \frac{{120}}{x} = 2\).
Đúng
Sai
c) Số xe thực tế là 15 xe.
Đúng
Sai
d) Thực tế mỗi xe chở 6 tấn hàng.
Đúng
Sai
Đáp án
a) Thực tế mỗi xe phải chở \(\frac{{90}}{x}\) tấn hàng.
Đúng
Sai
b) \(\frac{{90}}{x} - \frac{{120}}{x} = 2\).
Đúng
Sai
c) Số xe thực tế là 15 xe.
Đúng
Sai
d) Thực tế mỗi xe chở 6 tấn hàng.
Đúng
Sai
Phương pháp giải :
a) Biểu diễn số hàng mỗi xe cần chở thực tế theo x. b) Viết phương trình số hàng mỗi xe cần chở dự định và thực tế. c) Giải phương trình để tìm x, từ đó tính số xe thực tế. d) Khối lượng hàng mỗi xe chở thực tế = 120 : số xe thực tế. Lời giải chi tiết :
a) Theo dự định đội xe dùng \(x\) xe cùng loại để chở 120 tấn hàng nên mỗi xe cần chở \(\frac{{120}}{x}\) tấn hàng. Thực tế đội có số xe là: \(x + \frac{1}{3}x = \frac{4}{3}x\) (xe). Do đó, mỗi xe phải chở số tấn hàng là \(\frac{{120}}{{\frac{4}{3}x}} = \frac{{90}}{x}\) tấn hàng. Vậy khẳng định a) đúng. b) Vì so với dự định, mỗi xe phải chở ít hơn 2 tấn nên ta có phương trình: \(\frac{{120}}{x} - \frac{{90}}{x} = 2\) Vậy khẳng định b) sai. c) Giải phương trình: \(\begin{array}{l}\frac{{120}}{x} - \frac{{90}}{x} = 2\\\frac{{30}}{x} = 2\\x = \frac{{30}}{2} = 15\end{array}\) Do đó, đội xe dự định dùng 15 xe để chở hàng, thực tế thì đội dùng \(15.\frac{4}{3} = 20\) xe. Vậy khẳng định c) sai. d) Như vậy, thực tế mỗi xe chở \(120:20 = 6\) tấn hàng. Vậy khẳng định d) đúng, Đáp án a) Đ, b) S, c) S, d) Đ.
Câu 2 :
Một trường THCS cần mua x quyển vở và y cây bút để làm phần thưởng cho học sinh Xuất sắc và học sinh Giỏi. Mỗi quyển vở có giá niêm yết là 8 000 đồng, mỗi cây bút có giá niêm yết 6 000 đồng nên số tiền nhà trường cần chi trả là 11 triệu 200 nghìn đồng. Vì mua với số lượng lớn nên đại lý bán quyết định giảm giá 5% cho mỗi quyển vở và 6% cho mỗi cây bút, vì thế nhà trường chỉ cần trả 10 triệu 604 nghìn đồng. Biết 40% học sinh của trường là học sinh Xuất sắc và học sinh Giỏi, mỗi học sinh Xuất sắc được thưởng 5 quyển vở và 3 cây bút; mỗi học sinh Giỏi được thưởng 3 quyển vở và 2 cây bút. a) \(8\,000x + 6\,000y = 11\,200\,000\)
Đúng
Sai
b) \(7\,520x + 5\,700y = 10\,564\,000\)
Đúng
Sai
c) \(x = 950;y = 600\)
Đúng
Sai
d) Tổng số học sinh của trường là 600 học sinh.
Đúng
Sai
Đáp án
a) \(8\,000x + 6\,000y = 11\,200\,000\)
Đúng
Sai
b) \(7\,520x + 5\,700y = 10\,564\,000\)
Đúng
Sai
c) \(x = 950;y = 600\)
Đúng
Sai
d) Tổng số học sinh của trường là 600 học sinh.
Đúng
Sai
Phương pháp giải :
a) Viết phương trình biểu diễn số tiền nhà trường cần chi trả để mua x quyển vở và y cây bút. b) Viết phương trình biểu diễn số tiền nhà trường cần chi trả khi được giảm giá để mua x quyển vở và y cây bút. c) Giải hệ phương trình. d) Gọi số học sinh Xuất sắc là a (học sinh), số học sinh Giỏi là b (học sinh). \(\left( {a,b \in {N^*}} \right)\) Lập hệ phương trình biểu diễn số quyển vở và cây bút theo a và b, giải hệ phương trình để tính số học sinh Xuất sắc và học sinh Giỏi. Vì số học sinh Xuất sắc và học sinh Giỏi chiếm 40% tổng số học sinh nên ta tính số học sinh của trường = số học sinh Xuất sắc và học sinh Giỏi : 40%. Lời giải chi tiết :
a) Theo bài ra ta có mỗi quyển vở có giá niêm yết là 8000 đồng, mỗi cây bút có giá niêm yết 6000 đồng thì số tiền nhà trường cần chi trả là 11 triệu 200 nghìn đồng nên ta có phương trình: \(8\,000x + 6\,000y = 11\,200\,000\). (1) Vậy khẳng định a) đúng. b) Nếu giảm giá 5% cho mỗi quyển vở thì giá tiền mỗi quyển vở sau khi giảm là: \(8\,000.\left( {100\% - 5\% } \right) = 7\,600\) (đồng) Nếu giảm giá 6% cho mỗi cây bút thì giá tiền mỗi cây bút sau khi giảm là: \(6\,000.\left( {100\% - 6\% } \right) = 5\,640\) (đồng) Sau khi giảm giá thì nhà trường chỉ cần trả 10 triệu 604 nghìn đồng nên ta có phương trình: \(7\,600x + 5\,640y = 10\,604\,000\). (2) Vậy khẳng định b) sai. c) Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}8\,000x + 6\,000y = 11\,200\,000\\7\,600x + 5\,640y = 10\,604\,000\end{array} \right.\). Giải hệ phương trình ta được: \(x = 950;y = 600\). Vậy khẳng định c) đúng. d) Gọi số học sinh Xuất sắc là a (học sinh), số học sinh Giỏi là b (học sinh). \(\left( {a,b \in {N^*}} \right)\) Vì có 950 quyển vở, mỗi học sinh Xuất sắc được thưởng 5 quyển vở và mỗi học sinh Giỏi được thưởng 3 quyển vở nên ta có phương trình: \(5a + 3b = 950\) Vì có 600 cây bút, mỗi học sinh Xuất sắc được thưởng 3 cây bút và mỗi học sinh Giỏi được thưởng 2 cây bút nên ta có phương trình: \(3a + 2b = 600\) Ta có hệ phương trình: \(\left\{ \begin{array}{l}5a + 3b = 950\\3a + 2b = 600\end{array} \right.\). Giải hệ phương trình ta được \(a = 100,b = 150\). Suy ra tổng số học sinh Xuất sắc và học sinh Giỏi là: \(100 + 150 = 250\) (học sinh). Vì số học sinh Xuất sắc và học sinh Giỏi chiếm 40% tổng số học sinh tổng số học sinh của trường là: \(250:40\% = 625\) (học sinh). Vậy khẳng định d) sai. Đáp án a) Đ, b) S, c) Đ, d) S. a) Chu vi hình tam giác và hình chữ nhật lần lượt là \(3x + 18\) và \(4x + 16\).
Đúng
Sai
b) \(4x + 16 > 3x + 18\).
Đúng
Sai
c) \(x < 2\)
Đúng
Sai
d) Với x = 1 thì chu vi tam giác bằng diện tích hình chữ nhật.
Đúng
Sai
Đáp án
a) Chu vi hình tam giác và hình chữ nhật lần lượt là \(3x + 18\) và \(4x + 16\).
Đúng
Sai
b) \(4x + 16 > 3x + 18\).
Đúng
Sai
c) \(x < 2\)
Đúng
Sai
d) Với x = 1 thì chu vi tam giác bằng diện tích hình chữ nhật.
Đúng
Sai
Phương pháp giải :
a) Sử dụng công thức tính chu vi tam giác và chu vi hình chữ nhật. b) Vì chu vi hình tam giác lớn hơn chu vi hình chữ nhật nên ta viết được bất phương trình. c) Giải bất phương trình trên. d) Thay x = 1, kiểm tra xem khi đó chu vi tam giác có bằng diện tích hình chữ nhật không. Lời giải chi tiết :
a) Chu vi hình tam giác là: \(x + 3 + x + 5 + x + 10 = 3x + 18\). Chu vi hình chữ nhật là: \(2\left( {x + 2 + x + 6} \right) = 2\left( {2x + 8} \right) = 4x + 16\). Vậy khẳng định a) đúng. b) Vì chu vi hình tam giác lớn hơn chu vi hình chữ nhật nên ta có: \(3x + 18 > 4x + 16\). Vậy khẳng định b) sai. c) Giải bất phương trình: \(\begin{array}{l}3x + 18 > 4x + 16\\3x - 4x > 16 - 18\\ - x > - 2\\x < 2\end{array}\) Vậy khẳng định c) đúng. d) Với x = 1, chu vi hình tam giác là: \(3.1 + 18 = 3 + 18 = 21\). Diện tích hình chữ nhật là: \(\left( {x + 2} \right)\left( {x + 6} \right)\). Với x = 1 thì diện tích hình chữ nhật là: \(\left( {1 + 2} \right)\left( {1 + 6} \right) = 3.7 = 21\). Khi x = 1 thì chu vi hình tam giác bằng diện tích hình chữ nhật. Vậy khẳng định d) đúng. Đáp án a) Đ, b) S, c) Đ, d) Đ.
Câu 4 :
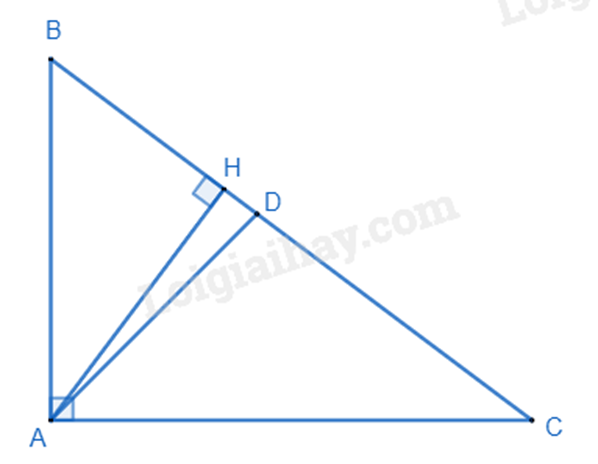
Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = 12cm, BC = 20cm. Vẽ AD là đường phân giác của góc BAC. a) Độ dài BH là 7,2cm.
Đúng
Sai
b) \(\sin DAC = \frac{{\sqrt 2 }}{2}\).
Đúng
Sai
c) \(\tan HAD \approx 7,12\).
Đúng
Sai
d) \(AH = BC.\sin B.\cos B\).
Đúng
Sai
Đáp án
a) Độ dài BH là 7,2cm.
Đúng
Sai
b) \(\sin DAC = \frac{{\sqrt 2 }}{2}\).
Đúng
Sai
c) \(\tan HAD \approx 7,12\).
Đúng
Sai
d) \(AH = BC.\sin B.\cos B\).
Đúng
Sai
Phương pháp giải :
a) Chứng minh $\Delta ABC\backsim \Delta HBA$ suy ra \(\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\) và tính BH. b) Dựa vào tính chất của tia phân giác của một góc, tính sin của góc đó. c) \(\widehat {BAD} = \widehat {BAH} + \widehat {HAD}\), tính góc \(\widehat {BAD},\widehat {BAH}\) suy ra \(\widehat {HAD}\), từ đó tính được \(\tan HAD\). d) Biến đổi \(BC.\sin B.\cos B\) thành AH. Lời giải chi tiết :
a) Xét tam giác ABC và tam giác HBA có: \(\widehat A = \widehat H\left( { = 90^\circ } \right)\) \(\widehat B\) chung Suy ra $\Delta ABC\backsim \Delta HBA$ (g.g) Suy ra \(\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\), do đó \(BH = \frac{{A{B^2}}}{{BC}} = \frac{{{{12}^2}}}{{20}} = 7,2\left( {cm} \right)\). Vậy khẳng định a) đúng. b) Vì AD là tia phân giác của góc BAC nên \(\widehat {BAD} = \widehat {DAC} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.90^\circ = 45^\circ \). Ta có \(\sin DAC = \sin 45^\circ = \frac{{\sqrt 2 }}{2}\). Vậy khẳng định b) đúng. c) Xét tam giác BHA, ta có: \(\sin BAH = \frac{{BH}}{{AB}} = \frac{{7,2}}{{12}} = \frac{3}{5}\) suy ra \(\widehat {BAH} \approx 37^\circ \) Ta có: \(\widehat {BAD} = \widehat {BAH} + \widehat {HAD}\) suy ra \(\widehat {HAD} = \widehat {BAD} - \widehat {BAH} \approx 45^\circ - 37^\circ = 8^\circ \). Suy ra \(\tan HAD = \tan 8^\circ \approx 0,14\left( {cm} \right)\). Vậy khẳng định c) sai. d) Ta có: \(BC.\sin B.\cos B = BC.\frac{{AH}}{{AB}}.\frac{{AB}}{{BC}} = AH\). Vậy khẳng định d) đúng. Đáp án a) Đ, b) Đ, c) S, d) Đ.
Phần III. Câu hỏi trắc nghiệm trả lời ngắn
Thí sinh trả lời câu hỏi từ câu 1 đến câu 6
Câu 1 :
Phương trình \({\left( {x - 3} \right)^2} - 4{x^2} = 0\) có hai nghiệm \({x_1};{x_2}\) \(\left( {{x_1} < {x_2}} \right)\). Tính giá trị của biểu thức \({x_1} + 3{x_2}\). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng hằng đẳng thức hiệu hai bình phương để giải phương trình tích. Lời giải chi tiết :
Ta có: \({\left( {x - 3} \right)^2} - 4{x^2} = 0\) \({\left( {x - 3} \right)^2} - {\left( {2x} \right)^2} = 0\) \(\begin{array}{l}\left( {x - 3 - 2x} \right)\left( {x - 3 + 2x} \right) = 0\\\left( { - x - 3} \right)\left( {3x - 3} \right) = 0\end{array}\) \( - x - 3 = 0\) hoặc \(3x - 3 = 0\) \(x = - 3\) hoặc \(x = 1\) Suy ra \({x_1} = - 3;{x_2} = 1\) Giá trị của biểu thức \({x_1} + 3{x_2}\) là: \({x_1} + 3{x_2} = - 3 + 3.1 = 0\). Đáp án: 0
Câu 2 :
Nghiệm \({x_0}\) của phương trình \(\frac{1}{{x - 2}} - \frac{2}{{x - 1}} = \frac{5}{{\left( {x - 2} \right)\left( {x - 1} \right)}}\) thỏa mãn biểu thức \(S = {x_0}^3 + 2{x_0}^2 + 2024\). Tính giá trị của S. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm điều kiện xác định. Giải phương trình chứa ẩn ở mẫu. Thay giá trị của x vào biểu thức S để tính. Lời giải chi tiết :
ĐKXĐ: \(x - 2 \ne 0\) và \(x - 1 \ne 0\) hay \(x \ne 2\) và \(x \ne 1\). Ta có: \(\frac{1}{{x - 2}} - \frac{2}{{x - 1}} = \frac{5}{{\left( {x - 2} \right)\left( {x - 1} \right)}}\) \(\begin{array}{l}\frac{{x - 1}}{{\left( {x - 2} \right)\left( {x - 1} \right)}} - \frac{{2\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x - 1} \right)}} = \frac{5}{{\left( {x - 2} \right)\left( {x - 1} \right)}}\\x - 1 - 2\left( {x - 2} \right) = 5\\x - 1 - 2x + 4 = 5\\ - x + 3 = 5\\x = 3 - 5\\x = - 2\end{array}\) Giá trị của biểu thức \(S = {x_0}^3 + 2{x_0}^2 + 2024\) tại \({x_0} = - 2\) là: \(S = {\left( { - 2} \right)^3} + 2{\left( { - 2} \right)^2} + 2024 \\= - 8 + 8 + 2024 = 2024.\) Đáp án: 2024
Câu 3 :
Hệ phương trình \(\left\{ \begin{array}{l}2\left( {x - 2y} \right) + 3\left( {x + 2y} \right) = 4\\\left( {x - y} \right) + 2\left( {x + y} \right) = 1\end{array} \right.\) có cặp nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\). Tính giá trị của biểu thức \(A = - 25{x_0} - 7{y_0}\). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Biến đổi hệ phương trình về dạng hệ hai phương trình bậc nhất hai ẩn và giải hệ phương trình đó. Thay giá trị \({x_0},{y_0}\) vào biểu thức A để tính giá trị của biểu thức. Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}2\left( {x - 2y} \right) + 3\left( {x + 2y} \right) = 4\\\left( {x - y} \right) + 2\left( {x + y} \right) = 1\end{array} \right.\) hay \(\left\{ \begin{array}{l}2x - 4y + 3x + 6y = 4\\x - y + 2x + 2y = 1\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}5x + 2y = 4\\3x + y = 1\end{array} \right.\) Nhân phương trình thứ hai với 2, ta được: \(\left\{ \begin{array}{l}5x + 2y = 4\\6x + 2y = 2\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}x = - 2\\3.\left( { - 2} \right) + y = 1\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}x = - 2\\y = 7\end{array} \right.\). Thay vào A, ta được: \(A = - 25.\left( { - 2} \right) - 7.7 = 1\). Đáp án: 1
Câu 4 :
Bạn An đăng ký tham gia khóa học tiếng Anh ở một trung tâm ngoại ngữ. Qua hai bài kiểm tra của khoá học, bạn An đã đạt lần lượt 62 và 67 điểm (thang điểm 100). Bạn phấn đấu đạt điểm trung bình ít nhất là 70 sau ba lần kiểm tra. Để có kết quà này, ở lần kiểm tra thứ ba, bạn An phải được ít nhất bao nhiêu điểm? (số điểm đạt được là các số tự nhiên). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Gọi số điểm bạn An đạt được ở lần kiểm tra thứ 3 là \(x\) \(\left( {x \in \mathbb{N},0 \le x \le 100} \right)\). Tính điểm trung bình của bạn An sau ba lần kiểm tra. Viết bất phương trình biểu diễn điểm trung bình ít nhất là 70 sau ba lần kiểm tra. Giải phương trình để tìm x nhỏ nhất. Lời giải chi tiết :
Gọi số điểm bạn An đạt được ở lần kiểm tra thứ 3 là \(x\) \(\left( {x \in \mathbb{N},0 \le x \le 100} \right)\). Điểm trung bình của bạn An sau ba lần kiểm tra là: \(\frac{{62 + 67 + x}}{3}\). Vì bạn phấn đấu đạt điểm trung bình ít nhất là 70 sau ba lần kiểm tra nên ta có: \(\begin{array}{l}\frac{{62 + 67 + x}}{3} \ge 70\\129 + x \ge 210\\x \ge 81\end{array}\) Vậy bạn An cần đạt ít nhất 81 điểm để đạt điểm trung bình ít nhất là 70 điểm. Đáp án: 81
Câu 5 :
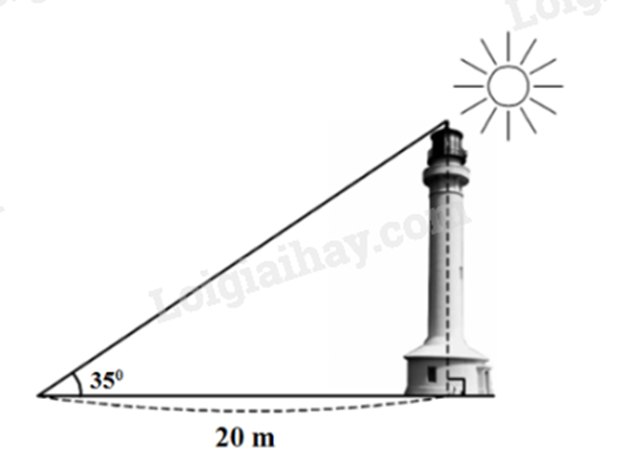
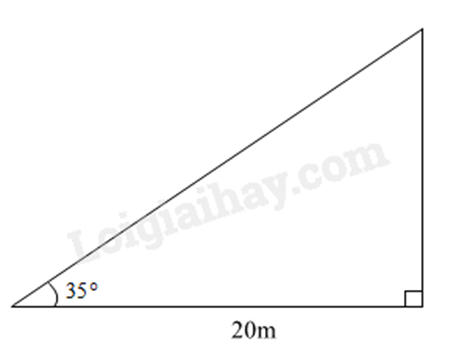
Hải đăng Trường Sa Lớn nằm trên đảo Trường Sa Lớn - “thủ phủ” quần đảo Trường Sa - có chiều cao bao nhiêu? Biết rằng tia nắng mặt trời chiếu qua đỉnh của ngọn hải đăng hợp với mặt đất 1 góc 35 độ và bóng của ngọn hải đăng trên mặt đất dài 20m. (làm tròn đến hàng đơn vị)
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng tỉ số lượng giác trong tam giác để tính chiều cao ngọn hải đăng. Lời giải chi tiết :
Chiều cao ngọn hải đăng là: \(20.\tan 35^\circ \approx 14\left( m \right)\). Đáp án: 14
Câu 6 :
Cho góc nhọn \(\alpha \) thỏa mãn \(0^\circ < \alpha < 50^\circ \). Rút gọn biểu thức \(A = \sin \left( {\alpha + 40^\circ } \right) - \sin \left( {\alpha + 30^\circ } \right) - \cos \left( {50^\circ - \alpha } \right) + \cos \left( {60^\circ - \alpha } \right)\) về biểu thức chỉ chứa tỉ số lượng giác sin của một góc. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng kiến thức về tỉ số lượng giác của hai góc phụ nhau: \(\cos \alpha = \sin \left( {90^\circ - \alpha } \right)\) Lời giải chi tiết :
Ta có: \(A = \sin \left( {\alpha + 40^\circ } \right) - \sin \left( {\alpha + 30^\circ } \right) - \cos \left( {50^\circ - \alpha } \right) + \cos \left( {60^\circ - \alpha } \right)\) \(\begin{array}{l} = \sin \left( {\alpha + 40^\circ } \right) - \sin \left( {\alpha + 30^\circ } \right) - \sin \left[ {90^\circ - \left( {50^\circ - \alpha } \right)} \right] + \cos \left[ {90^\circ - \left( {60^\circ - \alpha } \right)} \right]\\ = \sin \left( {\alpha + 40^\circ } \right) - \sin \left( {\alpha + 30^\circ } \right) - \sin \left( {40^\circ + \alpha } \right) + \sin \left( {30^\circ + \alpha } \right)\\ = \left[ {\sin \left( {\alpha + 40^\circ } \right) - \sin \left( {40^\circ + \alpha } \right)} \right] + \left[ { - \sin \left( {\alpha + 30^\circ } \right) + \sin \left( {30^\circ + \alpha } \right)} \right]\\ = 0 + 0 = 0\end{array}\) Đáp án: 0
|
























Danh sách bình luận