Đề kiểm tra giữa kì 2 Toán 11 - đề số 2 có lời giải chi tiết

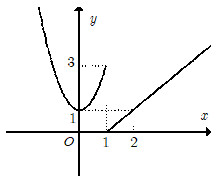
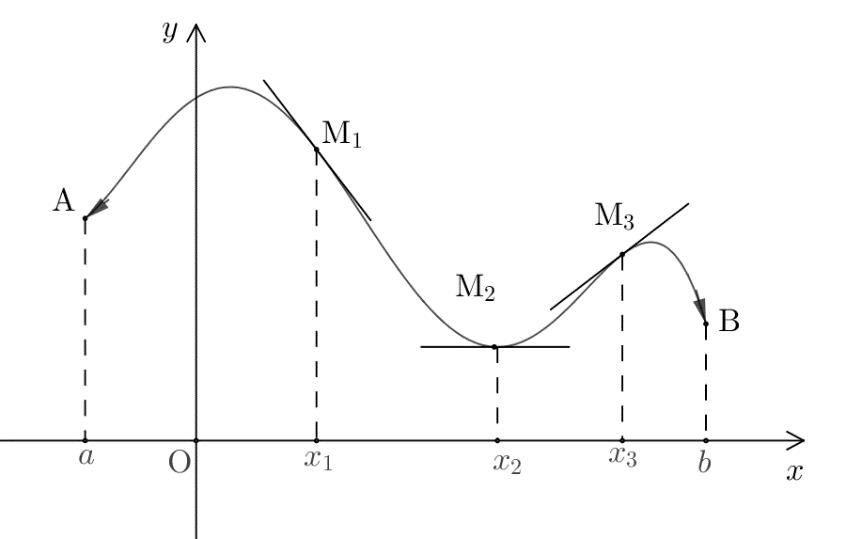
Đề bài

Câu 1. Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}$ và có đồ thị như hình vẽ. Hỏi hàm số $f\left( x \right)$ không liên tục tại điểm nào sau đây?

 

A. ${x_0} = 1$.          B. ${x_0} = 2$.          

C. ${x_0} = 3$.          D. ${x_0} = 0$.

Câu 2. Đạo hàm của hàm số $f\left( x \right) = {\left( {{x^2} + 1} \right)^4}$ tại điểm $x =  - 1$là

A. $64$.      B. $32$.     C. $- 64$.      D. $- 32$.

Câu 3. Khẳng định nào sau đây là khẳng định sai?

A. Nếu $d \bot \left( \alpha  \right)$ và $a//\left( \alpha  \right)$ thì $a \bot d$.

B. Nếu đường thẳng $d$ vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng $\left( \alpha  \right)$ thì $d$ vuông góc với bất kỳ đường thẳng nào nằm trong mặt phẳng $\left( \alpha  \right)$.

C. Nếu $d \bot \left( \alpha  \right)$ thì $d$ vuông góc với hai đường thẳng nằm trong $\left( \alpha  \right)$.

D. Nếu đường thẳng $d$ vuông góc với hai đường thẳng trong mặt phẳng $\left( \alpha  \right)$ thì $d \bot \left( \alpha  \right)$.

Câu 4. Trong các mệnh đề sau đây, mệnh đề nào sai?

A. Các hàm đa thức liên tục trên $\mathbb{R}$.

B. Các hàm phân thức hữu tỉ liên tục trên từng khoảng xác định của chúng.

C. Nếu hàm số $y = f\left( x \right)$ liên tục trên khoảng $\left( {a;b} \right)$ và $f\left( a \right).\,f\left( b \right) < 0$ thì phương trình $f\left( x \right) = 0$ có ít nhất một nghiệm thuộc $\left( {a;\,b} \right)$.

D. Nếu các hàm số $y = f\left( x \right)$, $y = g\left( x \right)$ liên tục tại ${x_0}$ thì hàm số $y = f\left( x \right).g\left( x \right)$ liên tục tại ${x_0}$.

Câu 5. Tính giới hạn $\lim \left( {\sqrt {9{n^2} + 2n}  - 3n + 8} \right)$ ta được kết quả:

A. $\dfrac{{25}}{3}$ .    B. $- \infty$. C. $\dfrac{1}{3}$.     D. $+ \infty$ .

Câu 6. Tính $\mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{2x + 1}}{{x - 3}}$ ta được kết quả.

A. $- \infty$ .           B. $+ \infty$ .      C. $6$.      D. $4$.

Câu 7. Trong không gian cho tứ diện đều$\overrightarrow {AC'}  = \dfrac{1}{2}\overrightarrow {AA'}  + \overrightarrow {AB}  + \overrightarrow {AD}$. Khẳng định nào sau đây là sai:

A. $\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC}$.          

B. $\overrightarrow {AD}  \bot \overrightarrow {DC}$.     

C. $\overrightarrow {AC}  \bot \overrightarrow {BD}$.        

D. $\overrightarrow {AD}  \bot \overrightarrow {BC}$.

Câu 8. Mệnh đề nào đúng trong các mệnh đề sau?

A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho (khi đường thẳng không vuông góc với mặt phẳng).

B. Góc giữa đường thẳng $a$ và mặt phẳng $\left( P \right)$ bằng góc giữa đường $b$ và mặt phẳng $\left( P \right)$ thì $a$ song song song hoặc trùng với $b$.

C. Góc giữa đường thẳng $a$ và mặt phẳng $\left( P \right)$ bằng góc giữa đường $a$ và mặt phẳng $\left( Q \right)$ thì mp$\left( P \right)$ song song với mp$\left( Q \right)$.

D. Góc giữa đường thẳng $a$ và mặt phẳng $\left( P \right)$ bằng góc giữa đường $b$ và mặt phẳng $\left( P \right)$ thì $a$ song song song với $b$.

Câu 9. Mệnh đề nào đúng trong các mệnh đề sau?

A. Góc giữa hai đường thẳng $a$ và $b$ bằng góc giữa hai đường thẳng $a$ và $c$ thì $b$ song song với $c$.

B. Góc giữa hai đường thẳng bằng góc giữa hai vec tơ chỉ phương của hai đường thẳng đó.

C. Góc giữa hai đường thẳng là góc nhọn.

D. Góc giữa hai đường thẳng $a$ và $b$ bằng góc giữa hai đường thẳng $a$ và $c$ khi $b$ song song hoặc trùng với $c$.

Câu 10. Biết $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + ax}  - 1}}{x} = 3,\,\,\,\,\left( {a \in \mathbb{R}} \right)$, tìm giá trị của $a$?

A. $a = 3$ .    B. $a = 0$ .            C. $a = 6$.     D. $a = 4$.

Câu 11. Cho $\mathop {\lim }\limits_{x \to \,{x_0}} f\left( x \right) = L;$ $\,\mathop {\lim }\limits_{x \to \,{x_0}} g\left( x \right) = M$, với $L,M \in \mathbb{R}$. Chọn khẳng định sai.

A. $\mathop {\lim }\limits_{x \to \,{x_0}} \left[ {f\left( x \right) - g\left( x \right)} \right] = L - M$. 

B. $\mathop {\lim }\limits_{x \to \,{x_0}} \left[ {f\left( x \right).g\left( x \right)} \right] = L.M$.

C. $\mathop {\lim }\limits_{x \to \,{x_0}} \dfrac{{f\left( x \right)}}{{g\left( x \right)}} = \dfrac{L}{M}$.   

D. $\mathop {\lim }\limits_{x \to \,{x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M$.

Câu 12. Cho đồ thị của hàm số $f\left( x \right)$ trên khoảng $\left( {a;\,\,b} \right)$. Biết rằng tiếp tuyến của đồ thị hàm số $f\left( x \right)$ tại các điểm ${M_1};\,\,{M_2};\,\,{M_3}$ như hình vẽ.

 

Khi đó xét dấu $f'\left( {{x_1}} \right)\,,f'\left( {{x_2}} \right)\,,f'\left( {{x_3}} \right)$.

A. $f'\left( {{x_1}} \right) = 0,\,\,f'\left( {{x_2}} \right) < 0,\,\,f'\left( {{x_3}} \right) > 0$ 

B. $f'\left( {{x_1}} \right) < 0,\,\,f'\left( {{x_2}} \right) > 0,\,\,f'\left( {{x_3}} \right) = 0$.

C. $f'\left( {{x_1}} \right) < 0,\,\,f'\left( {{x_2}} \right) = 0,\,\,f'\left( {{x_3}} \right) > 0$.

D. $f'\left( {{x_1}} \right) > 0,\,\,f'\left( {{x_2}} \right) = 0,\,\,f'\left( {{x_3}} \right) < 0$.

Câu 13. Tính giới hạn $\lim \dfrac{{{5^n} - {{3.4}^n}}}{{{{6.7}^n} + {8^n}}}$ ta được kết quả:

A. $- \infty$.      B. $0$.       C. $\dfrac{1}{6}$ .    D. $+ \infty$ .

Câu 14. Tìm $a$ để hàm số $f\left( x \right) = \left\{ \begin{array}{l}{x^2} + ax + 2{\rm{      khi  }}x > 1\\2{x^2} - x + 3a{\rm{    khi  }}x \le 1\end{array} \right.$ có giới hạn tại $x = 1$.

A. $a = 0$ .      B. $a = 1$.     

C. $a = 4$.     D. $a = 3$ .

Câu 15. Trong không gian cho đường thẳng $\Delta$  và điểm $O$. Qua $O$ có bao nhiêu đường thẳng vuông góc với $\Delta$?

A. 1.         B. Vô số.      C. 2.      D. 3.

Câu 16. Cho hàm số $y = {x^3} - 3{x^2} + 2$ có đồ thị $\left( C \right)$. Tiếp tuyến của đồ thị $\left( C \right)$ tại điểm có hoành độ bằng 3 có dạng $ax + by - 25 = 0$. Khi đó, tổng $a + b$ bằng:

A. $8$.        B. $- 10$.       C. $- 8$.        D. $10$.

Câu 17. Trong không gian cho hai đường thẳng $CC'$ và $b$ lần lượt có vectơ chỉ phương là $\overrightarrow u ,\,\,\overrightarrow v$. Gọi $\alpha$ là góc giữa hai đường thẳng $a$ và $b$. Khẳng định nào sau đây là đúng:

A. $\cos \alpha  = \cos \left( {\overrightarrow u ;\overrightarrow v } \right)$    

B. $\overrightarrow u .\overrightarrow v  = \sin \alpha$. 

C. $\alpha  = \left| {\left( {\overrightarrow u ,\overrightarrow v } \right)} \right|$ 

D. $\cos \alpha  = \left| {\cos \left( {\overrightarrow u ,\overrightarrow v } \right)} \right|$

Câu 18. Hình hộp chữ nhật có 3 kích thước là $2;\,\,3;\,\,4$ thì độ dài đường chéo của nó là

A. $\sqrt {29}$          B. $\sqrt {30}$          C. $5$             D. $\sqrt {28}$

Câu 19. Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {x + 4}  - 2}}{x}\,\,\,\,\,\,\,\,{\rm{khi}}\,\,x > 0\\m{x^2} + 2m + \dfrac{1}{4}\,\,\,{\rm{khi}}\,\,x \le 0\end{array} \right.$, với $m$ là tham số. Gọi ${m_0}$ là giá trị của tham số $m$ để hàm số $f\left( x \right)$ liên tục tại $x = 0$. Hỏi ${m_0}$ thuộc khoảng nào dưới đây?

A. $\left( { - \dfrac{3}{2}; - \dfrac{1}{4}} \right)$.  B. $\left( {\dfrac{1}{2};1} \right)$.   C. $\left( { - \dfrac{1}{4};\dfrac{1}{2}} \right)$.  D. $\left( {1;2} \right)$.

Câu 20. Cho hàm số $y = f\left( x \right) = \sqrt {x - 1}$. Trong các mệnh đề sau đây, có bao nhiêu mệnh đề đúng?

I. Hàm số $f\left( x \right)$ có tập xác định là $\left[ {1; + \infty } \right)$.          

II. Hàm số $f\left( x \right)$ liên tục trên $\left[ {1; + \infty } \right)$.

III. Hàm số $f\left( x \right)$ gián đoạn tại $x = 1$.

IV. Hàm số $f\left( x \right)$ liên tục tại $x = 0$ .

A. $0$.     B. $1$.        C. $2$.          D. 3.

Câu 21. Cho tứ diện $ABCD$ với trọng tâm $G$. Chọn mệnh đề đúng

A. $\overrightarrow {AG}  = \dfrac{1}{3}\left( {\overrightarrow {BA}  + \overrightarrow {BC}  + \overrightarrow {BD} } \right)$      

B. $\overrightarrow {AG}  = \dfrac{1}{4}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {CD} } \right)$

C. $\overrightarrow {AG}  = \dfrac{1}{4}\left( {\overrightarrow {BA}  + \overrightarrow {BC}  + \overrightarrow {BD} } \right)$      

D. $\overrightarrow {AG}  = \dfrac{1}{4}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right)$

Câu 22. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh $SA = a\sqrt 3$, $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Góc giữa đường thẳng $CD$ và mặt phẳng $\left( {SBC} \right)$ là:

A. ${90^o}$                    B. ${45^o}$                 

C. ${30^o}$                    D. ${60^0}$

Câu 23. Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và $\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = 3$. Tính $\mathop {\lim }\limits_{x \to 2} \dfrac{{{f^3}\left( x \right) + 3f\left( x \right) - 4}}{{{x^2} - 2x}}$

A. $36$                       B. $27$                      

C. $\dfrac{{27}}{2}$             D. $4$.

Câu 24. Tìm tất cả các giá trị của tham số $m$ để phương trình $\left( {2{m^2} - 5m + 2} \right){\left( {x - 1} \right)^{18}}\left( {{x^{81}} - 2} \right) + 2x + 3 = 0$ có nghiệm:

A. $m \in \mathbb{R}$. 

B. $m \in \mathbb{R}\backslash \left\{ {\dfrac{1}{2}\,;\,2} \right\}$           

C. $m \in \left\{ {\dfrac{1}{2}\,;\,2} \right\}$. 

D. $m \in \left\{ {0;\dfrac{1}{2}\,;\,2} \right\}$.

Câu 25. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi, cạnh bên $SA = AB$ và $SA$ vuông góc với $BC$. Góc giữa hai đường thẳng $SD$ và $BC$ là?

A. ${45^o}$                  B. ${30^o}$                  

C. ${60^0}$                   D. ${90^o}$

Lời giải chi tiết

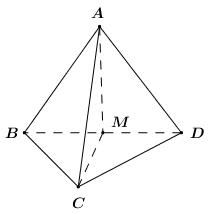
Câu 1 (NB) – Hàm số liên tục

Phương pháp:

Dựa vào đồ thị hàm số xác định điểm mà tại đó đồ thị hàm số bị đứt đoạn (không liền mạch).

Cách giải:

Dựa vào đồ thị hàm số ta thấy hàm số không liên tục tại ${x_0} = 1$.

Chọn A.

Câu 2 (TH) – Quy tắc tính đạo hàm

Phương pháp:

- Sử dụng công thức tính đạo hàm: $\left( {{u^n}} \right)' = n.{u^{n - 1}}.u'$.

- Thay $x =  - 1$ vào $f'\left( x \right)$ và tính $f'\left( { - 1} \right)$.

Cách giải:

Ta có: $f\left( x \right) = {\left( {{x^2} + 1} \right)^4}$ $\Rightarrow f'\left( x \right) = 4{\left( {{x^2} + 1} \right)^3}.2x = 8x{\left( {{x^2} + 1} \right)^3}$.

$\Rightarrow f'\left( { - 1} \right) =  - 8.{\left( {1 + 1} \right)^3} =  - 64$.

Chọn C.

Câu 3 (TH) – Đường thẳng vuông góc với mặt phẳng

Phương pháp:

Đọc từng đáp án và sử dụng các định lí về đường vuông góc với mặt.

Cách giải:

Dễ thấy đáp án D sai vì $d$ phải vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng $\left( \alpha  \right)$ thì $d \bot \left( \alpha  \right)$

Chọn D.

Câu 4 (TH) – Hàm số liên tục

Phương pháp:

Sử dụng các định lí về hàm số liên tục.

Cách giải:

Dễ thấy các đáp án A, B, D đúng.

Phát biểu C đúng phải là: Nếu hàm số $y = f\left( x \right)$ liên tục trên khoảng $\left[ {a;b} \right]$ và $f\left( a \right).\,f\left( b \right) < 0$ thì phương trình $f\left( x \right) = 0$ có ít nhất một nghiệm thuộc $\left( {a;\,b} \right)$.

Chọn C.

Câu 5 (TH) – Giới hạn của dãy số

Phương pháp:

Nhân liên hợp sau đó chia cả tử và mẫu cho $n$.

Cách giải:

Ta có:

$\begin{array}{l}\,\,\,\,\lim \left( {\sqrt {9{n^2} + 2n}  - 3n + 8} \right)\\ = \lim \dfrac{{9{n^2} + 2n - {{\left( {3n - 8} \right)}^2}}}{{\sqrt {9{n^2} + 2n}  + 3n - 8}}\\ = \lim \dfrac{{9{n^2} + 2n - 9{n^2} + 48n - 64}}{{\sqrt {9{n^2} + 2n}  + 3n - 8}}\\ = \lim \dfrac{{50n - 64}}{{\sqrt {9{n^2} + 2n}  + 3n - 8}}\\ = \lim \dfrac{{50 - \dfrac{{64}}{n}}}{{\sqrt {9 + \dfrac{2}{n}}  + 3 - \dfrac{8}{n}}} = \dfrac{{50}}{{3 + 3}} = \dfrac{{25}}{3}\end{array}$

Chọn A.

Chú ý khi giải: Các em HS có thể sử dụng MTCT như sau:

Nhập dãy số:

CALC $X = {10^{10}}$  ta được kết quả:  $= \dfrac{{25}}{3}$.

Câu 6 (TH) – Giới hạn của hàm số

Phương pháp:

Sử dụng quy tắc tính giới hạn một bên.

Cách giải:

Ta có:

$\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {3^ + }} \left( {2x + 1} \right) = 2.3 + 1 = 7 > 0\\\mathop {\lim }\limits_{x \to {3^ + }} \left( {x - 3} \right) = 0;\,\,\,x \to {3^ + } \Rightarrow x - 3 > 0\end{array} \right.$  $\Rightarrow \mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{2x + 1}}{{x - 3}} =  + \infty$.

Chọn B.

Câu 7 (TH) – Đường thẳng vuông góc với mặt phẳng

Phương pháp:

- Sử dụng quy tắc 3 điểm cộng vectơ.

- Sử dụng định lí chứng minh đường thẳng vuông góc với mặt phẳng: $\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)$.

- Sử dụng định lí: $\left\{ \begin{array}{l}d \bot \left( P \right)\\a \subset \left( P \right)\end{array} \right. \Rightarrow d \bot a$.

Cách giải:

 

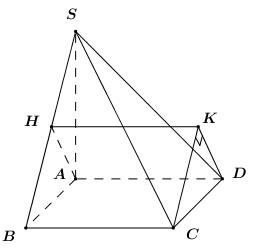
Vì $\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC}$ nên đáp án A đúng.

Gọi $M$ là trung điểm của $BD$.

Vì $\Delta ABD,\,\,\Delta BCD$ là các tam giác đều nên $\left\{ \begin{array}{l}AM \bot BD\\CM \bot BD\end{array} \right. \Rightarrow BD \bot \left( {AMC} \right) \Rightarrow BD \bot AC$.

$\Rightarrow \overrightarrow {BD}  \bot \overrightarrow {AC}  \Rightarrow$ Đáp án C đúng.

Chứng minh tương tự ta có $\overrightarrow {AD}  \bot \overrightarrow {BC}  \Rightarrow$ Đáp án D đúng.

Chọn B.

Câu 8 (TH) – Đường thẳng vuông góc với mặt phẳng

Phương pháp:

Sử dụng định lí: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.

Cách giải:

Mệnh đề đúng là: Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho (khi đường thẳng không vuông góc với mặt phẳng).

Chọn A.

Câu 9 (NB) – Vectơ trong không gian

Phương pháp:

Đọc từng đáp án và chọn mệnh đề đúng.

Cách giải:

Trong các đáp án chỉ có đáp án C là đúng.

Chọn C.

Câu 10 (TH) – Giới hạn của hàm số

Phương pháp:

- Nhân liên hợp và rút gọn để khử dạng $\dfrac{0}{0}$.

- Sau khi đã khử được dạng $\dfrac{0}{0}$, thay $x = 0$ để tính giới hạn. Giải phương trình tìm $a$.

Cách giải:

Ta có:

$\begin{array}{l}\,\,\,\,\,\,\mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {1 + ax}  - 1}}{x} = 3\\ \Leftrightarrow \mathop {\lim }\limits_{x \to 0} \dfrac{{1 + ax - 1}}{{x\left( {\sqrt {1 + ax}  + 1} \right)}} = 3\\ \Leftrightarrow \mathop {\lim }\limits_{x \to 0} \dfrac{a}{{\sqrt {1 + ax}  + 1}} = 3\\ \Leftrightarrow \dfrac{a}{2} = 3 \Leftrightarrow a = 6\end{array}$

Chọn C.

Câu 11 (NB) – Giới hạn của hàm số

Phương pháp:

Sử dụng các định lí về giới hạn.

Cách giải:

Khẳng định sai là $\mathop {\lim }\limits_{x \to \,{x_0}} \dfrac{{f\left( x \right)}}{{g\left( x \right)}} = \dfrac{L}{M}$ vì không có điều kiện $M \ne 0$.

Chọn C.

Câu 12 (TH) – Định nghĩa và ý nghĩa của đạo hàm

Phương pháp:

Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ $x = {x_0}$ là $k = f'\left( {{x_0}} \right)$.

Cách giải:

- Tiếp tuyến tại ${M_1}$ là đường thẳng nghịch biến trên $\mathbb{R}$ nên $f'\left( {{x_1}} \right) < 0$.

- Tiếp tuyến tại ${M_2}$ là đường thẳng song song với trục hoành nên $f'\left( {{x_2}} \right) = 0$.

- Tiếp tuyến tại ${M_3}$ là đường thẳng đồng biến trên $\mathbb{R}$ nên $f'\left( {{x_3}} \right) > 0$.

Vậy $f'\left( {{x_1}} \right) < 0,\,\,\,f'\left( {{x_2}} \right) = 0,\,\,f'\left( {{x_3}} \right) > 0$.

Chọn C.

Câu 13 (TH) – Giới hạn của dãy số

Phương pháp:

Chia cả tử và mẫu cho ${8^n}$.

Cách giải:

Ta có: $\lim \dfrac{{{5^n} - {{3.4}^n}}}{{{{6.7}^n} + {8^n}}} = \lim \dfrac{{{{\left( {\dfrac{5}{8}} \right)}^n} - 3.{{\left( {\dfrac{1}{2}} \right)}^n}}}{{6.{{\left( {\dfrac{7}{8}} \right)}^n} + 1}} = 0$.

Chọn B.

Câu 14 (TH) – Giới hạn của hàm số

Phương pháp:

Hàm số $y = f\left( x \right)$ có giới hạn tại $x = {x_0}$ khi và chỉ khi $\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right)$.

Cách giải:

Ta có:

$\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} + ax + 2} \right) = 3 + a\\\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {2{x^2} - x + 3a} \right) = 1 + 3a\end{array}$.

Để hàm số $y = f\left( x \right)$ có giới hạn tại $x = 1$ thì $\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) \Leftrightarrow 3 + a = 1 + 3a \Leftrightarrow a = 1$.

Chọn B.

Câu 15 (TH) – Đường thẳng vuông góc với mặt phẳng

Phương pháp:

- Qua một điểm nằm ngoài đường thẳng vẽ được duy nhất 1 mặt phẳng vuông góc với đường thẳng đã cho.

- Sử dụng định lí: $\left\{ \begin{array}{l}d \bot \left( P \right)\\a \subset \left( P \right)\end{array} \right. \Rightarrow d \bot a$.

Cách giải:

Qua $O$ vẽ được duy nhất một mặt phẳng $\left( P \right)$ sao cho $\left( P \right) \bot \Delta$.

Trong $\left( P \right)$ có vô số đường thẳng $d$ đi qua $O$, khi đó ta có $\left\{ \begin{array}{l}\Delta  \bot \left( P \right)\\d \subset \left( P \right)\end{array} \right. \Rightarrow \Delta  \bot d$.

Vậy qua $O$ vẽ được vô số đường thẳng vuông góc với D.

Chọn B.

Câu 16 (TH) – Quy tắc tính đạo hàm

Phương pháp:

- Tiếp tuyến của đồ thị hàm số $y = f\left( x \right)$ tại điểm có hoành độ $x = {x_0}$ là:

$y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)$

- Đồng nhất hệ số tìm $a,\,\,b$ và tính tổng $a + b$.

Cách giải:

Ta có: $y' = 3{x^2} - 6x \Rightarrow y'\left( 3 \right) = 9$ và $y\left( 3 \right) = 2$.

Khi đó ta có phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng 3 là:

$y = 9\left( {x - 3} \right) + 2 \Leftrightarrow y = 9x - 25 \Leftrightarrow 9x - y - 25 = 0$.

$\Leftrightarrow \left\{ \begin{array}{l}a = 9\\b =  - 1\end{array} \right.$. Vậy $a + b = 9 + \left( { - 1} \right) = 8$.

Chọn A.

Câu 17 (NB) – Hai đường thẳng vuông góc

Phương pháp:

Trong không gian cho hai đường thẳng $CC'$ và $b$ lần lượt có vectơ chỉ phương là $\overrightarrow u ,\,\,\overrightarrow v$. Gọi $\alpha$ là góc giữa hai đường thẳng $a$ và $b$. Khi đó: $\cos \alpha  = \left| {\cos \left( {\overrightarrow u ,\overrightarrow v } \right)} \right|$.

Cách giải:

Trong không gian cho hai đường thẳng $CC'$ và $b$ lần lượt có vectơ chỉ phương là $\overrightarrow u ,\,\,\overrightarrow v$. Gọi $\alpha$ là góc giữa hai đường thẳng $a$ và $b$. Khi đó: $\cos \alpha  = \left| {\cos \left( {\overrightarrow u ,\overrightarrow v } \right)} \right|$.

Chọn D.

Câu 18 (NB) – Vectơ trong không gian

Phương pháp:

Hình hộp chữ nhật có 3 kích thước là $a,\,\,b,\,\,c$ thì độ dài đường chéo của nó là $\sqrt {{a^2} + {b^2} + {c^2}}$.

Cách giải:

Hình hộp chữ nhật có 3 kích thước là $2;\,\,3;\,\,4$ thì độ dài đường chéo của nó là $\sqrt {{2^2} + {3^2} + {4^2}}  = \sqrt {29}$.

Chọn A.

Câu 19 (VD) – Hàm số liên tục

Phương pháp:

Hàm số $y = f\left( x \right)$ liên tục tại điểm $x = {x_0}$ khi và chỉ khi $\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = f\left( {{x_0}} \right)$.

Cách giải:

Ta có:

$\begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{\sqrt {x + 4}  - 2}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{x + 4 - 4}}{{x\left( {\sqrt {x + 4}  + 2} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{1}{{\sqrt {x + 4}  + 2}} = \dfrac{1}{{2 + 2}} = \dfrac{1}{4}\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {m{x^2} + 2m + \dfrac{1}{4}} \right) = 2m + \dfrac{1}{4}\\f\left( 0 \right) = 2m + \dfrac{1}{4}\end{array}$

Để hàm số liên tục tại $x = 0$ thì $\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right)$.

$\Rightarrow \dfrac{1}{4} = 2m + \dfrac{1}{4} \Leftrightarrow m = 0 = {m_0}$.

Vậy ${m_0} \in \left( { - \dfrac{1}{4};\dfrac{1}{2}} \right)$.

Chọn C.

Câu 20 (TH) – Hàm số liên tục

Phương pháp:

Hàm căn thức liên tục trên các khoảng xác định của chúng.

Cách giải:

TXĐ: $x - 1 \ge 0 \Leftrightarrow x \ge 1$.

Do đó hàm số $f\left( x \right)$ có tập xác định $\left[ {1; + \infty } \right)$ và hàm số $f\left( x \right)$ cũng liên tục trên $\left[ {1; + \infty } \right)$.

$\Rightarrow$ Mệnh đề I, II đúng và mệnh đề III, IV sai.

Vậy số mệnh đề đúng là 2.

Chọn C.

Câu 21 (TH) – Vectơ trong không gian

Phương pháp:

Cho tứ diện $ABCD$ với trọng tâm $G$. Ta có: $\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0$.

Cách giải:

Vì $G$ là trọng tâm của tứ diện $ABCD$ nên $\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0$.

$\begin{array}{l} \Leftrightarrow \overrightarrow {GA}  + \overrightarrow {GA}  + \overrightarrow {AB}  + \overrightarrow {GA}  + \overrightarrow {AC}  + \overrightarrow {GA}  + \overrightarrow {AD}  = \overrightarrow 0 \\ \Leftrightarrow 4\overrightarrow {AG}  = \overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} \\ \Rightarrow \overrightarrow {AG}  = \dfrac{1}{4}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right)\end{array}$

Chọn D.

Câu 22 (VD) – Đường thẳng vuông góc với mặt phẳng

Phương pháp:

- Dựng $AH \bot SB$, chứng minh $AH \bot \left( {SBC} \right)$.

- Dựng $DK//AH\,\,\left( {K \in \left( {SBC} \right)} \right)$, xác định góc giữa $CD$ và $\left( {SBC} \right)$ là góc giữa $DC$ và hình chiếu của $DC$ lên $\left( {SBC} \right)$.

- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.

Cách giải:

 

Trong $\left( {SAB} \right)$ kẻ $AH \bot SB\,\,\left( {H \in SB} \right)$ ta có:

$\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\\\left\{ \begin{array}{l}AH \bot BC\,\,\left( {cmt} \right)\\AH \bot SB\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right)\end{array}$

Dựng $DK//AH\,\,\left( {K \in \left( {SBC} \right)} \right) \Rightarrow DK \bot \left( {SBC} \right)$.

$\Rightarrow CK$ là hình chiếu của $CD$ lên $\left( {SBC} \right)$.

$\Rightarrow \angle \left( {CD;\left( {SBC} \right)} \right) = \angle \left( {CD;CK} \right) = \angle DCK$.

Vì $AD//BC \Rightarrow AD//\left( {SBC} \right)$ $\Rightarrow d\left( {A;\left( {SBC} \right)} \right) = d\left( {D;\left( {SBC} \right)} \right) \Rightarrow AH = DK$.

Áp dụng hệ thức lượng trong tam giác vuông $SAB$ ta có: $AH = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \dfrac{{a\sqrt 3 .a}}{{\sqrt {3{a^2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{2} = DK$.

Vì $DK \bot \left( {SBC} \right)\,\,\left( {cmt} \right) \Rightarrow DK \bot CK$ $\Rightarrow \Delta CDK$ vuông tại $K$.

Ta có: $\sin \angle DCK = \dfrac{{DK}}{{CD}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \angle DCK = {60^0}$.

Vậy $\angle \left( {CD;\left( {SBC} \right)} \right) = {60^0}$.

Chọn D.

Câu 23 (VDC) – Giới hạn của hàm số

Phương pháp:

- Đặt $\dfrac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = g\left( x \right)$, biểu diễn $f\left( x \right)$ theo $g\left( x \right)$ và tính $\mathop {\lim }\limits_{x \to 2} f\left( x \right)$.

- Phân tích biểu thức $\dfrac{{{f^3}\left( x \right) + 3f\left( x \right) - 4}}{{{x^2} - 2x}}$ thành tích 2 phân thức, 1 phân thức dạng $\dfrac{0}{0}$ và một phân thức xác định.

- Dựa vào giới hạn đề bài.

Cách giải:

Đặt $\dfrac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = g\left( x \right) \Rightarrow f\left( x \right) = \left( {{x^2} - x - 2} \right)g\left( x \right) + 1$.

Khi đó ta có: $\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = 3 \Rightarrow \mathop {\lim }\limits_{x \to 2} g\left( x \right) = 3$.

$\Rightarrow \mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \left[ {\left( {{x^2} - x - 2} \right)g\left( x \right) + 1} \right] = 1$.

Ta có:

$\begin{array}{l}\,\,\,\,\mathop {\lim }\limits_{x \to 2} \dfrac{{{f^3}\left( x \right) + 3f\left( x \right) - 4}}{{{x^2} - 2x}}\\ = \mathop {\lim }\limits_{x \to 2} \dfrac{{\left[ {f\left( x \right) - 1} \right]\left[ {{f^2}\left( x \right) + f\left( x \right) + 4} \right]}}{{x\left( {x - 2} \right)}}\\ = \mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{x - 2}}.\mathop {\lim }\limits_{x \to 2} \dfrac{{{f^2}\left( x \right) + f\left( x \right) + 4}}{x}\end{array}$

Theo bài ra ta có:

$\begin{array}{l}\,\,\,\,\,\,\,\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = 3\\ \Rightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} = 3\\ \Leftrightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{x - 2}}.\dfrac{1}{{x + 1}} = 3\\ \Leftrightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{x - 2}}.\mathop {\lim }\limits_{x \to 2} \dfrac{1}{{x + 1}} = 3\\ \Leftrightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{x - 2}}.\dfrac{1}{3} = 3\\ \Leftrightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 1}}{{x - 2}} = 9\end{array}$

Vậy $\mathop {\lim }\limits_{x \to 2} \dfrac{{{f^3}\left( x \right) + 3f\left( x \right) - 4}}{{{x^2} - 2x}} = 9.\dfrac{{1 + 1 + 4}}{2} = 27$.

Chọn B.

Câu 24 (VD) – Hàm số liên tục

Phương pháp:

Phương trình đa thức bậc lẻ luôn có nghiệm.

Cách giải:

TH1: $2{m^2} - 5m + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{1}{2}\\m = 2\end{array} \right.$, khi đó phương trình trở thành $2x + 3 = 0 \Leftrightarrow x =  - \dfrac{3}{2}$.

$\Rightarrow$ phương trình có nghiệm.

$\Rightarrow m = \dfrac{1}{2};\,\,m = 2$ thỏa mãn.

TH2: $2{m^2} - 5m + 2 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne \dfrac{1}{2}\\m \ne 2\end{array} \right.$, phương trình $\left( {2{m^2} - 5m + 2} \right){\left( {x - 1} \right)^{18}}\left( {{x^{81}} - 2} \right) + 2x + 3 = 0$ là phương trình đa thức bậc lẻ nên luôn có nghiệm.

Vậy phương trình đã cho có nghiệm với mọi $m \in \mathbb{R}$.

Chọn A. 

Câu 25 (VD) – Hai đường thẳng vuông góc

Phương pháp:

Sử dụng định lí: $\angle \left( {a;b} \right) = \angle \left( {a;c} \right)$ với $b//c$.

Cách giải:

 

Vì $AD//BC \Rightarrow \angle \left( {SD;BC} \right) = \angle \left( {SD;AD} \right)$.

Ta có: $\angle \left( {SA;BC} \right) = \angle \left( {SA;AD} \right) = {90^0}$ (Do $BC//AD$).

$\Rightarrow \Delta SAD$ vuông tại $A$.

Lại có: $SA = AB\,\,\left( {gt} \right)$, $AB = AD$ (do $ABCD$ là hình thoi) $\Rightarrow SA = AD$.

$\Rightarrow \Delta SAD$ vuông cân tại $A$.

$\Rightarrow \angle SDA = {45^0} \Rightarrow \angle \left( {SD;AD} \right) = {45^0}$.

Vậy $\angle \left( {SD;BC} \right) = {45^0}$.

Chọn A.

Loigiaihay.com