Đề kiểm tra giữa kì 2 Toán 11 - đề số 1 có lời giải chi tiết

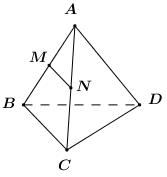
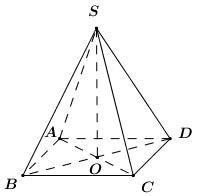
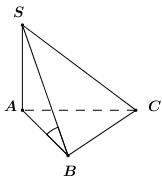
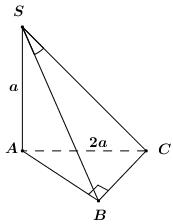
Đề bài

A. TRẮC NGHIỆM (4 điểm)

Câu 1. Cho cấp số nhân \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} = 2\) và công bội \(q =  - 3\). Giá trị của \({u_3}\) bằng:

A. \(27\)           B. \( - 27\)        C. \( - 9\)         D. \(18\)

Câu 2. Cho cấp số cộng \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} =  - 5\) và công sai \(d = 3\). Tổng của 50 số hạng đầu tiên là:

A. \(2345\)       B. \(6850\)       C. \(3425\)       D. \(3500\)

Câu 3. Cho cấp số nhân \(\left( {{v_n}} \right)\) thỏa mãn \(\left\{ \begin{array}{l}{v_2} = 2\\{v_5} = 16\end{array} \right.\). Khi đó ta có:

A. \({v_1} =  - 2\)       B. \({v_4} = \dfrac{1}{2}\)   C. \({v_6} = 64\)        D. \({v_7} = 64\)

Câu 4. Cho dãy số \(\left( {{u_n}} \right)\) với \(\left\{ \begin{array}{l}{u_1} = \dfrac{1}{2}\\{u_n} = \dfrac{1}{{2 - {u_{n - 1}}}},\,\,\forall n > 1\end{array} \right.\). Giá trị của \({u_4}\) bằng:

A. \(\dfrac{3}{4}\)     B. \(\dfrac{4}{5}\)     C. \(\dfrac{5}{6}\)     D. \(\dfrac{5}{4}\)

Câu 5. Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_n} = \dfrac{{2n + 1}}{{n + 1}},\,\,\forall n \ge 1\). Khẳng định nào sau đây là sai?

A. \(\left( {{u_n}} \right)\) là dãy số bị chặn dưới   

B. \({u_5} = \dfrac{{11}}{6}\)

C. \(\left( {{u_n}} \right)\) là dãy giảm                    

D. \(\left( {{u_n}} \right)\) là dãy tăng và bị chặn  

Câu 6. Với số thực \(a\) cho trước, giá trị của \(\lim \dfrac{{a.n + 2}}{{2n + 1}}\) là:

A. \(a\)             B. \(2a\)           C. \(\dfrac{a}{2}\)     D. \(1\)

Câu 7. Giá trị của \(\lim \left( {\sqrt {{n^2} - 2n - 2}  - n} \right)\) là:

A. \( - 1\)         B. \( - \dfrac{2}{3}\) C. \( - \infty \) D. \( + \infty \)

Câu 8. Giá trị của \(\lim \dfrac{{{4^n} + {6^n}}}{{{6^{n - 1}} - {5^n}}}\) là:

A. \(0\)             B. \( + \infty \)             C. \(6\)             D. \(\dfrac{1}{6}\)

Câu 9. Cho tứ diện \(ABCD\) có \(M\) là trung điểm \(AB,\,\,N\) là trung điểm \(AC\). Mệnh đề nào sau đây đúng?

A. Ba vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} ,\,\,\overrightarrow {AD} \) đồng phẳng   

B. Ba vectơ \(\overrightarrow {BA} ,\,\,\overrightarrow {CB} ,\,\,\overrightarrow {BD} \) đồng phẳng

C. Ba vectơ \(\overrightarrow {BD} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {MN} \) đồng phẳng  

D. Ba vectơ \(\overrightarrow {AD} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {MN} \) đồng phẳng  

Câu 10. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\). Biết rằng \(SA = SB = SC = SD\). Khẳng định nào sau đây là sai?

A. \(AB//\left( {SCD} \right)\)           B. \(AC \bot \left( {SBD} \right)\)    

C. \(SO \bot \left( {ABCD} \right)\) D. \(AD \bot \left( {SAB} \right)\)

Câu 11. Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = a\). Khi đó góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {ABC} \right)\) có số đo là:

A. \({30^0}\)   B. \({45^0}\)  

C. \({135^0}\)             D. \({60^0}\)

Câu 12. Cho hình chóp \(S.ABC\). Đáy \(ABC\) là tam giác vuông cân tại \(B,\,\,AC = 2a\). Đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), \(SA = a\). Khi đó, cosin của góc tạo bởi \(SC\) và mặt phẳng \(\left( {SAB} \right)\) có giá trị là:

A. \(\dfrac{{\sqrt {15} }}{5}\)          B. \(\sqrt {\dfrac{2}{5}} \)   

C. \(\sqrt {\dfrac{2}{3}} \)    D. \(\dfrac{1}{{\sqrt 3 }}\)

B – TỰ LUẬN (6 điểm)

Bài 1 (3 điểm):

a) Cho cấp số cộng \(\left( {{u_n}} \right)\) với công sai \(d\). Biết rằng \(\left\{ \begin{array}{l}{u_3} + {u_5} = 2d - 2\\u_2^2 + u_4^2 = 20\end{array} \right.\). Tìm số hạng đầu và công sai của cấp số cộng.

b) Tính giới hạn \(\lim \left( {2n - \sqrt[3]{{8{n^3} + 5{n^2}}}} \right)\).

Bài 2 (3 điểm)

Cho hình chóp tứ giác \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\). Biết \(AB = BC = a\) và \(AD = 2a\). Đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\), \(SA = a\). Kẻ \(AH \bot SB\) và \(AK \bot SC\) \(\left( {H \in SB,\,\,K \in SC} \right)\).

a) Chứng minh \(AH \bot \left( {SBC} \right)\).

b) Chứng minh \(SC \bot HK\) và \(DC \bot \left( {SAC} \right)\).

c) Tính góc giữa hai đường thẳng \(HK\) và \(CD\).

Lời giải chi tiết

 

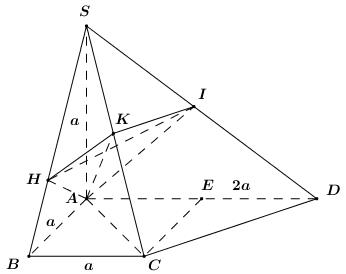
Câu 1 (NB) – Cấp số nhân

Phương pháp:

Sử dụng công thức SHTQ của cấp số nhân có số hạng đầu \({u_1}\), công bội \(q\) là \({u_n} = {u_1}{q^{n - 1}}\).

Cách giải:

Ta có: \({u_3} = {u_1}.{q^2} = 2.{\left( { - 3} \right)^2} = 18\).

Chọn D.

Câu 2 (NB) – Cấp số cộng

Phương pháp:

Sử dụng công thức tính tổng \(n\) số hạng đầu tiên của CSC có số hạng đầu \({u_1}\), công sai \(d\) là \({S_n} = \dfrac{{\left[ {2{u_1} + \left( {n - 1} \right)d} \right]n}}{2}\).

Cách giải:

Ta có: \({S_{50}} = \dfrac{{\left[ {2.\left( { - 5} \right) + \left( {50 - 1} \right).3} \right].50}}{2} = 3425\).

Chọn C.

Câu 3 (TH) – Cấp số nhân

Phương pháp:

Sử dụng công thức SHTQ của cấp số nhân có số hạng đầu \({u_1}\), công bội \(q\) là \({u_n} = {u_1}{q^{n - 1}}\).

Cách giải:

Gọi số hạng đầu là \({v_1}\) và công bội là \(q\), ta có: \(\left\{ \begin{array}{l}{v_2} = 2\\{v_5} = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{v_1}q = 2\\{v_1}{q^4} = 16\end{array} \right.\).

Chia vế theo vế 2 phương trình trên ta có \({q^3} = 8 \Leftrightarrow q = 2\).

\( \Rightarrow 2{v_1} = 2 \Leftrightarrow {v_1} = 1\).

Khi đó ta có \(\left\{ \begin{array}{l}{v_4} = {v_1}{q^3} = {1.2^3} = 8\\{v_6} = {v_1}{q^5} = {1.2^5} = 32\\{v_7} = {v_1}{q^6} = {1.2^6} = 64\end{array} \right.\).

Vậy đáp án đúng là D.

Chọn D.

Câu 4 (NB) – Dãy số

Phương pháp:

Tính lần lượt \({u_2},\,\,{u_3},\,\,{u_4}\) nhờ công thức truy hồi của dãy số.

Cách giải:

Ta có:

\(\begin{array}{l}{u_2} = \dfrac{1}{{2 - {u_1}}} = \dfrac{1}{{2 - \dfrac{1}{2}}} = \dfrac{2}{3}\\{u_3} = \dfrac{1}{{2 - {u_2}}} = \dfrac{1}{{2 - \dfrac{2}{3}}} = \dfrac{3}{4}\\{u_4} = \dfrac{1}{{2 - {u_3}}} = \dfrac{2}{{2 - \dfrac{3}{4}}} = \dfrac{4}{5}\end{array}\)

Chọn B.

Câu 5 (TH) – Dãy số

Phương pháp:

Xét hiệu \(H = {u_{n + 1}} - {u_n}\).

+ Nếu \(H > 0\,\,\forall n \ge 1\) thì dãy \(\left( {{u_n}} \right)\) là dãy số tăng.

+ Nếu \(H < 0\,\,\forall n \ge 1\) thì dãy \(\left( {{u_n}} \right)\) là dãy số giảm.

Cách giải:

Xét hiệu

\(\begin{array}{l}H = {u_{n + 1}} - {u_n},\,\,\forall n \ge 1\\\,\,\,\,\,\, = \dfrac{{2\left( {n + 1} \right) + 1}}{{n + 1 + 1}} - \dfrac{{2n + 1}}{{n + 1}}\\\,\,\,\,\,\, = \dfrac{{2n + 3}}{{n + 2}} - \dfrac{{2n + 1}}{{n + 1}}\\\,\,\,\,\,\, = \dfrac{{\left( {2n + 3} \right)\left( {n + 1} \right) - \left( {2n + 1} \right)\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\\,\,\,\,\,\, = \dfrac{{2{n^2} + 5n + 3 - 2{n^2} - 5n - 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\\,\,\,\,\,\, = \dfrac{1}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0\,\,\forall n \ge 1\end{array}\)

Do đó dãy số \(\left( {{u_n}} \right)\) là dãy số tăng.

Vậy đáp án sai là C.

Chọn C.

Câu 6 (NB) – Giới hạn của dãy số

Phương pháp:

Chia cả tử và mẫu cho \(n\).

Cách giải:

Ta có: \(\lim \dfrac{{a.n + 2}}{{2n + 1}} = \lim \dfrac{{a + \dfrac{2}{n}}}{{2 + \dfrac{1}{n}}} = \dfrac{a}{2}\).

Chọn C.

Câu 7 (TH) – Giới hạn của dãy số

Phương pháp:

- Nhân liên hợp.

- Chia cả tử và mẫu cho \(n\).

Cách giải:

Ta có:

\(\begin{array}{l}\,\,\,\,\,\lim \left( {\sqrt {{n^2} - 2n - 2}  - n} \right)\\ = \lim \dfrac{{{n^2} - 2n - 2 - {n^2}}}{{\sqrt {{n^2} - 2n - 2}  + n}}\\ = \lim \dfrac{{ - 2n - 2}}{{\sqrt {{n^2} - 2n - 2}  + n}}\\ = \lim \dfrac{{ - 2 - \dfrac{2}{n}}}{{\sqrt {1 - \dfrac{2}{n} - \dfrac{2}{{{n^2}}}}  + 1}} =  - 1\end{array}\).

Chọn A.

Câu 8 (TH) – Giới hạn của dãy số

Phương pháp:

Chia cả tử và mẫu cho \({6^n}\).

Cách giải:

Ta có:  \(\lim \dfrac{{{4^n} + {6^n}}}{{{6^{n - 1}} - {5^n}}} = \lim \dfrac{{{{\left( {\dfrac{2}{3}} \right)}^n} + 1}}{{\dfrac{1}{6} - {{\left( {\dfrac{5}{6}} \right)}^n}}} = 6\).

Chọn C.

Câu 9 (TH) – Vectơ trong không gian

Phương pháp:

- Sử dụng tính chất đường phân giác của tam giác.

- Sử dụng định lí: Trong không gian cho hai vectơ \(\overrightarrow a ,\,\,\overrightarrow b \) không cùng phương và vectơ \(\overrightarrow c \). Khi đó ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) đồng phẳng khi và chỉ khi tồn tại cặp số \(m,\,\,n\) sao cho \(\overrightarrow c  = m\overrightarrow a  + n\overrightarrow b \). Cặp số \(m,\,\,n\) là duy nhất.

Cách giải:

 

Ta có: \(MN\) là đường trung bình của \(\Delta ABC\) nên \(\overrightarrow {MN}  = \dfrac{1}{2}\overrightarrow {BC}  = \dfrac{1}{2}\left( {\overrightarrow {BD}  - \overrightarrow {CD} } \right)\).

Do đó ba vectơ \(\overrightarrow {BD} ,\,\,\overrightarrow {CD} ,\,\,\overrightarrow {MN} \) đồng phẳng.

Chọn C.

Câu 10 (NB) – Đường thẳng vuông góc với mặt phẳng

Phương pháp:

Sử dụng định lí \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\).

Cách giải:

 

Vì \(SA = SC \Rightarrow \Delta SAC\) cân tại \(S \Rightarrow SO \bot AC\).

Vì \(SB = SD \Rightarrow \Delta SBD\) cân tại \(S \Rightarrow SO \bot BD\).

\( \Rightarrow SO \bot \left( {ABCD} \right)\).

Chọn C.

Câu 11 (TH) – Đường thẳng vuông góc với mặt phẳng

Phương pháp:

- Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.

- Sử dụng tỉ số lượng giác để tính góc.

Cách giải:

 

Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow AB\) là hình chiếu của \(SB\) lên \(\left( {ABC} \right)\).

\( \Rightarrow \angle \left( {SB;\left( {ABC} \right)} \right) = \angle \left( {SB;AB} \right) = \angle SBA\).

Xét tam giác vuông \(SAB\) ta có: \(SA = AB = a \Rightarrow \Delta SAB\) vuông cân tại \(A\).

Vậy \(\angle \left( {SB;\left( {ABC} \right)} \right) = \angle SBA = {45^0}\).

Chọn B.

Câu 12 (VD) – Đường thẳng vuông góc với mặt phẳng

Phương pháp:

- Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.

- Sử dụng định lí Pytago và tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.

Cách giải:

 

Ta có: \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\).

\( \Rightarrow SB\) là hình chiếu vuông góc của \(SC\) lên \(\left( {SAB} \right)\).

\( \Rightarrow \angle \left( {SC;\left( {SAB} \right)} \right) = \angle \left( {SC;SB} \right) = \angle BSC\).

Vì \(BC \bot \left( {SAB} \right)\,\,\left( {cmt} \right) \Rightarrow BC \bot SB\) \( \Rightarrow \Delta SBC\) vuông tại \(B\) 

Tam giác \(ABC\) vuông cân tại \(B\) \( \Rightarrow AB = BC = \dfrac{{AC}}{{\sqrt 2 }} = \dfrac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \).

Xét tam giác vuông \(SAB\) có: \(SB = \sqrt {S{A^2} + A{B^2}}  = \sqrt {{a^2} + 2{a^2}}  = a\sqrt 3 \).

\( \Rightarrow SC = \sqrt {S{B^2} + C{B^2}}  =  a\sqrt 5 \)

Xét tam giác vuông \(SBC\) có: \(\cos \angle BSC = \dfrac{{SB}}{{SC}} = \dfrac{{a\sqrt 3 }}{{a\sqrt 5 }} = \sqrt {\dfrac{3}{5}} = \dfrac {\sqrt{15}}{5}\). 

Chọn A.

B – TỰ LUẬN (6 điểm)

Bài 1 (VD) – Cấp số cộng – Giới hạn của dãy số

Phương pháp:

a) Sử dụng công thức số hạng tổng quát \({u_n} = {u_1} + \left( {n - 1} \right)d\) và tính chất cấp số cộng \({u_{n - 1}} + {u_{n + 1}} = 2{u_n}\). Đưa hệ phương trình đã cho về hệ 2 ẩn \({u_4},\,\,d\). Giải hệ tìm \({u_4},\,\,d\). Sau đó tìm \({u_1} = {u_4} - 3d\).

b) Nhân liên hợp, sử dụng hằng đẳng thức \({a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\). Sau đó chia cả tử và mẫu cho \(n\) với số mũ cao nhất.

Cách giải:

a) Theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\,\left\{ \begin{array}{l}{u_3} + {u_5} = 2d - 2\\u_2^2 + u_4^2 = 20\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2{u_4} = 2d - 2\\u_2^2 + u_4^2 = 20\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{u_4} = d - 1\\{\left( {{u_4} - 2d} \right)^2} + u_4^2 = 20\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{u_4} = d - 1\\{\left( {d - 1 - 2d} \right)^2} + {\left( {d - 1} \right)^2} = 20\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{u_4} = d - 1\\{d^2} + 2d + 1 + {d^2} - 2d + 1 = 20\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{u_4} = d - 1\\2{d^2} = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_4} = d - 1\\d =  \pm 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{u_4} = 2\\d = 3\end{array} \right.\\\left\{ \begin{array}{l}{u_4} =  - 4\\d =  - 3\end{array} \right.\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{u_1} = {u_4} - 3d =  - 7\\d = 3\end{array} \right.\\\left\{ \begin{array}{l}{u_1} = {u_4} - 3d = 5\\d =  - 3\end{array} \right.\end{array} \right.\end{array}\)

Vậy \({u_1} =  - 7;\,\,d = 3\) hoặc \({u_1} = 5;\,\,d =  - 3\).

b) Ta có:

\(\begin{array}{l}\,\,\,\,\lim \left( {2n - \sqrt[3]{{8{n^3} + 5{n^2}}}} \right)\\ = \lim \dfrac{{8{n^3} - 8{n^3} - 5{n^2}}}{{4{n^2} + 2n\sqrt[3]{{8{n^3} + 5{n^2}}} + {{\left( {\sqrt[3]{{8{n^3} + 5{n^2}}}} \right)}^2}}}\\ = \lim \dfrac{{ - 5{n^2}}}{{4{n^2} + 2n\sqrt[3]{{8{n^3} + 5{n^2}}} + {{\left( {\sqrt[3]{{8{n^3} + 5{n^2}}}} \right)}^2}}}\\ = \lim \dfrac{{ - 5}}{{4 + 2\sqrt[3]{{8 + \dfrac{5}{n}}} + {{\left( {\sqrt[3]{{8 + \dfrac{5}{n}}}} \right)}^2}}}\\ = \dfrac{{ - 5}}{{4 + 2.2 + {2^2}}} = \dfrac{{ - 5}}{{12}}\end{array}\)

Bài 2 (VDC) – Đường thẳng vuông góc với mặt phẳng

Phương pháp:

a) Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot a\\d \bot b\\a \cap b \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( P \right)\).

b) Sử dụng định lí: \(\left\{ \begin{array}{l}d \bot \left( P \right)\\a \subset \left( P \right)\end{array} \right. \Rightarrow d \bot a\) để chứng minh \(SC \bot HK\).

Gọi \(E\) là trung điểm của \(AD\), chứng minh \(DC \bot AC\), từ đó chứng minh \(DC \bot \left( {SAC} \right)\).

c) Trong \(\left( {SCD} \right)\) kẻ \(KI//CD\,\,\left( {I \in SD} \right)\), khi đó ta có \(\angle \left( {HK;CD} \right) = \angle \left( {HK;KI} \right)\).

Tính \(\angle HKI = \angle AKH + \angle AKI\). Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông và tính chất 2 đường thẳng vuông góc để tính góc.

Cách giải:

 

a) Ta có: \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\)

\(\left\{ \begin{array}{l}AH \bot SB\,\,\left( {gt} \right)\\AH \bot BC\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right)\).

b) Vì \(AH \bot \left( {SBC} \right)\,\,\left( {cmt} \right) \Rightarrow AH \bot SC\).

Ta có: \(\left\{ \begin{array}{l}AH \bot SC\,\,\left( {cmt} \right)\\AK \bot SC\,\,\left( {gt} \right)\end{array} \right.\) \( \Rightarrow SC \bot \left( {AHK} \right) \Rightarrow SC \bot HK\).

Gọi \(E\) là trung điểm của \(AD\), khi đó \(ABCE\) là hình vuông cạnh \(a\).

\( \Rightarrow CE = a = \dfrac{1}{2}AD \Rightarrow \Delta ACD\) vuông tại \(C\) \( \Rightarrow AC \bot CD\).

Ta có: \(\left\{ \begin{array}{l}DC \bot AC\,\,\left( {cmt} \right)\\DC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\)\( \Rightarrow DC \bot \left( {SAC} \right)\).

c) Trong \(\left( {SCD} \right)\) kẻ \(KI//CD\,\,\left( {I \in SD} \right)\), khi đó ta có \(\angle \left( {HK;CD} \right) = \angle \left( {HK;KI} \right)\).

Áp dụng hệ thức lượng trong tam giác vuông \(SAB\) ta có:

\(\begin{array}{l}AH = \dfrac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }}\\ = \dfrac{{a.a}}{{\sqrt {{a^2} + {a^2}} }} = \dfrac{{a\sqrt 2 }}{2}\end{array}\).

Áp dụng hệ thức lượng trong tam giác vuông \(SAC\) ta có:

\(\begin{array}{l}AK = \dfrac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }}\\ = \dfrac{{a.a\sqrt 2 }}{{\sqrt {{a^2} + 2{a^2}} }} = \dfrac{{a\sqrt 6 }}{3}\end{array}\).

Vì \(AH \bot \left( {SBC} \right)\,\,\left( {cmt} \right)\) \( \Rightarrow AH \bot HK \Rightarrow \Delta AHK\) vuông tại \(H\)

\(\begin{array}{l} \Rightarrow \sin \angle AKH = \dfrac{{AH}}{{AK}}\\ = \dfrac{{a\sqrt 2 }}{2}:\dfrac{{a\sqrt 6 }}{3} = \dfrac{{\sqrt 3 }}{2}\\ \Rightarrow \angle AKH = {60^0}\end{array}\)

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}KI//CD\\CD \bot \left( {SAC} \right)\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow KI \bot \left( {SAC} \right)\\ \Rightarrow KI \bot AK\end{array}\)

\( \Rightarrow \angle AKI = {90^0}\).

\(\begin{array}{l} \Rightarrow \angle HKI = \angle AKH + \angle AKI\\ = {60^0} + {90^0} = {150^0} > {90^0}\end{array}\).

Vậy

\(\begin{array}{l}\angle \left( {HK;CD} \right) = \angle \left( {HK;KI} \right)\\ = {180^0} - \angle HKI = {180^0} - {150^0} = {30^0}\end{array}\).

Loigiaihay.com