Đề kiểm tra 15 phút - Đề số 1 - Bài 9 - Chương 3 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 9 - Chương 3 - Hình học 9 Quảng cáo
Đề bài Cho tam giác cân ABC có \(\widehat B = 120^\circ \), \(AC = 6cm\). Tính độ dài đường tròn ngoại tiếp tam giác. Phương pháp giải - Xem chi tiết Sử dụng +Tỉ số lượng giác của góc nhọn +Góc nội tiếp bằng nửa góc ở tâm Lời giải chi tiết
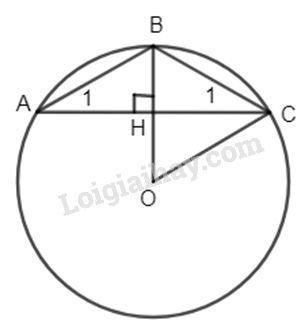
Ta có: \(BA = BC\; (gt)\) \( \Rightarrow \widehat {{A_1}} = \widehat {{C_1}} = \dfrac{{180^\circ - 120^\circ } }{ 2} = 30^\circ \) Vẽ đường cao BH ta có BH đồng thời là trung tuyến hay \(HA = HC = 3\,cm.\) Trong tam giác vuông ABH ta có : \(AB = \dfrac{{AH} }{ {\cos 30^\circ }} \Rightarrow AB = \dfrac{3}{{\dfrac{{\sqrt 3 } }{ 2}}} = 2\sqrt 3 \) (cm) Gọi O là tâm đường tròn ngoại tiếp ta có : \(\widehat {BOC} = 2\widehat {BAC} = 60^\circ \). Vậy tam giác BOC đều \(AB = BC = OB = 2\sqrt 3 \)(cm). Độ dài đường tròn ngoại tiếp tam giác ABC là : \(C = 2\pi R = 2\pi 2\sqrt 3 = 4\pi \sqrt 3 \)(cm). Loigiaihay.com
|




















Danh sách bình luận