Đề kiểm tra 15 phút - Đề số 1 - Bài 3 - Chương 2 - Hình học 9

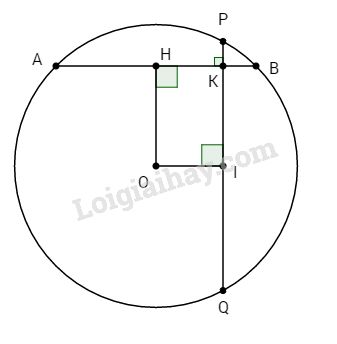
Đề bài

Cho đường tròn (O; 10cm), dây AB = 16cm

a. Tính khoảng cách từ tâm O đến dây AB. 

b. Lấy K thuộc dây AB sao cho AK = 14cm. Vẽ dây PQ vuông góc với AB tại K. Chứng tỏ : AB = PQ.

Lời giải chi tiết

a. Kẻ \(OH ⊥ AB\), ta có: 

\(HA = HB = {{AB} \over 2} = {{16} \over 2} = 8\,\left( {cm} \right)\) (quan hệ giữa đường kính và dây cung)

Xét tam giác vuông AOH, ta có:

\(OH = \sqrt {O{A^2} - A{H^2}}  = \sqrt {{{10}^2} - {8^2}}\)\(\;  = 6\,\left( {cm} \right)\)

b. Ta có: \(KB = AB -AK = 16 - 14 = 2\; (cm)\)

Do đó: \(HK = HB - KB = 8 - 2 = 6 \;(cm)\)

Kẻ \(OI ⊥ PQ\), khi đó tứ giác OHKI là hình chữ nhật có hai cạnh kề \(OH = KH = 6\;(cm)\) nên là hình vuông.

Do đó: \(OH = OI = 6\;(cm) \)\(⇒ AB = PQ\) (định lí).

Loigiaihay.com