Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 2 - Hình học 9

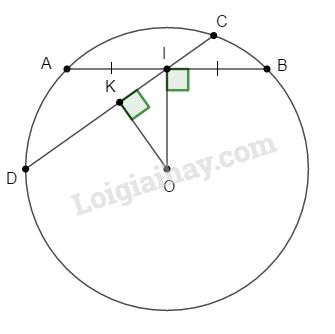
Đề bài

Gọi I là trung điểm của dây cung AB không qua tâm của đường tròn (O; R). Qua I vẽ dây cung CD.

a. Chứng tỏ \(CD ≥ AB\). Tìm độ dài nhỏ nhất, lớn nhất của các dây quanh I.

b. Cho \(R = 5cm, OI = 4cm.\) Tính độ dài dây cung ngắn nhất qua I.

c. Chứng tỏ rằng : \(\widehat {OAI} > \widehat {ODI}\)

Lời giải chi tiết

a. Kẻ \(OK ⊥ CD\), ta có: \(∆OKI\) vuông nên \(OI ≥ OK\) (cạnh huyền > cạnh góc vuông)

\(⇒ CD ≥ AB\) (định lí 2)

Dấu “=” xảy ra khi \(CD = AB.\) Do đó độ dài nhỏ nhất của CD bằng AB hay CD trùng với AB. Hiển nhiên đường kính qua I là dây lớn nhất.

b. Ta có: \(∆OIA\) vuông tại I

\( \Rightarrow AI = \sqrt {O{A^2} - O{I^2}}  \)\(\;= \sqrt {{5^2} - {4^2}}  = 3\,\left( {cm} \right)\)

Do đó dây cung \(AB = 6cm\)

c. \(\sin \widehat {OAI} = {{OI} \over {OA}} = {{OI} \over R};\)\(\,\sin \widehat {ODI} = {{OK} \over {OD}} = {{OK} \over R}\)

Mà \(OI > OK \Rightarrow {{OI} \over R} > {{OK} \over R}\) hay \(\sin \widehat {OAI} > \sin \widehat {ODI} \Rightarrow \widehat {OAI} > \widehat {ODI}\)

 Loigiaihay.com