Câu hỏi 1 trang 135 SGK Đại số và Giải tích 11Cho hai hàm số.... Quảng cáo
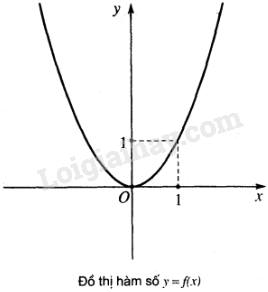
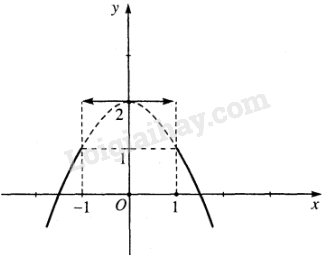
Video hướng dẫn giải Cho hai hàm số f(x) = x2 và \(g(x) = \left\{ \matrix{- {x^2} + 2;\,\,\,x \le - 1 \hfill \cr 2;\,\,\,\, - 1 < x < 1 \hfill \cr - {x^2} + 2;\,\,\,x \ge 1 \hfill \cr} \right.\) có đồ thị như hình 55
LG a Tính giá trị của mỗi hàm số tại \(x=1\) và so sánh với giới hạn (nếu có) của hàm số đó khi \(x \to 1\); Phương pháp giải: Thay \(x=1\) vào lần lượt hai hàm số và tính giá trị. Lời giải chi tiết: \(f(1) = {1^2} = 1 = \mathop {\lim }\limits_{x \to 1} f(x)\) Vì \(x=1\) nên \(g(1) =-1^2+ 1 = -1 + 1 = 0\) Lại có: \(\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( { - {x^2} + 2} \right) = 1\) và \(\mathop {\lim }\limits_{x \to {1^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( 2 \right) = 2\) nên \(\mathop {\lim }\limits_{x \to {1^ - }} g\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right)\) và không tồn tại giới hạn \(\mathop {\lim }\limits_{x \to 1} g\left( x \right)\) LG b Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ \(x = 1\) Phương pháp giải: Quan sát đồ thị và nhận xét. Lời giải chi tiết: Đồ thị hàm số \(f(x)\) liên tục tại \(x = 1\) Đồ thị hàm số \(g(x) \) gián đoạn tại \(x = 1\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
