Câu 6.39 trang 203 SBT Đại số 10 Nâng cao

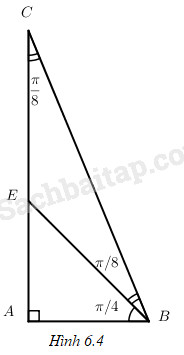
Đề bài

Tính \(\cos \dfrac{\pi }{8}\) và \(\sin \dfrac{\pi }{8}\) bằng phương pháp hình học như sau:

Xét tam giác vuông ABC với 

\(\widehat A = \dfrac{\pi }{2};\widehat C = \dfrac{\pi }{8}\) thì \(\cos \dfrac{\pi }{8} = \dfrac{{AC}}{{BC}};\sin \dfrac{\pi }{8} = \dfrac{{AB}}{{BC}}\).

Bằng cách xét điểm E trên cạnh AC sao cho \(AE = AB\) (h. 6.4), hãy chứng minh rằng:

\(\cos \dfrac{\pi }{8} = \dfrac{{\sqrt {2 + \sqrt 2 } }}{2},\sin \dfrac{\pi }{8} = \dfrac{{\sqrt {2 - \sqrt 2 } }}{2}\)

Lời giải chi tiết

Coi AB có độ dài là 1 thì dễ thấy \(AE = AB = 1,BE = CE = \sqrt 2 ;\)

\(AC = AE + EC = 1 + \sqrt 2 ;\)

\(BC = \sqrt {1 + {{\left( {1 + \sqrt 2 } \right)}^2}}  = \sqrt {2\left( {2 + \sqrt 2 } \right)}.\)

Từ đó \(\cos \dfrac{\pi }{8} = \dfrac{{AC}}{{BC}} = \dfrac{{1 + \sqrt 2 }}{{\sqrt {2\left( {2 + \sqrt 2 } \right)} }} = \dfrac{{\sqrt {2 + \sqrt 2 } }}{2};\)

\(\sin \dfrac{\pi }{8} = \dfrac{{AB}}{{BC}} = \dfrac{1}{{\sqrt {2\left( {2 + \sqrt 2 } \right)} }} = \dfrac{{\sqrt {2 - \sqrt 2 } }}{2}.\)

Loigiaihay.com