Giải SBT toán hình học và giải tích 12 nâng cao

Câu 4.55 trang 184 sách bài tập Giải tích 12 Nâng cao

Trong mặt phằng phức xét ngũ giác đều ABCDE nội tiếp đường tròn đơn vị. A là điểm biểu diễn số 1

Quảng cáo

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

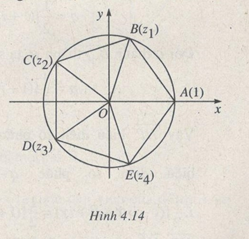
Trong mặt phẳng phức xét ngũ giác đều ABCDE nội tiếp đường tròn đơn vị. A là điểm biểu diễn số 1 (giả sử đi dọc chu vi đa giác theo ngược chiều kim đồng hồ gặp các đỉnh kế tiếp B, C, D, E). Kí hiệu \({z_1},{z_2},{z_3},{z_4}\) là các số phức theo thứ tự biểu diễn bởi các điểm B, C, D, E.

LG a

Chứng minh rằng \(1,{z_1},{z_2},{z_3},{z_4}\) là các nghiệm của phương trình \({z^5} - 1 = 0\) và \({z_1} + {1 \over {{z_1}}} = 2\cos {{2\pi } \over 5}\)

Giải chi tiết:

\({z_1} = \cos {{2\pi } \over 5} + i\sin {{2\pi } \over 5},{z_2} = \cos {{4\pi } \over 5} + i\sin {{4\pi } \over 5}\)

\({z_3} = \cos {{6\pi } \over 5} + i\sin {{6\pi } \over 5},{z_4} = \cos {{8\pi } \over 5} + i\sin {{8\pi } \over 5}\)

Từ đó theo công thức Moa-vrơ, \(1,{z_1},{z_2},{z_3},{z_4}\) là nghiệm các phương trình \({z^5} - 1 = 0\) (đó là tất cả các nghiệm vì phương trình có bậc 5).

\({z_1} + {1 \over {{z_1}}} = {z_1} + {\bar z_1} = 2\cos {{2\pi } \over 5}\)

LG b

Viết \({z^5} - 1 = \left( {z - 1} \right)\left( {{z^4} + {z^3} + {z^2} + z + 1} \right)\) rồi đưa phương trình \({z^4} + {z^3} + {z^2} + z + 1 = 0\) về phương trình bậc hai đối với ẩn phụ \({\rm{w}} = z + {1 \over z}\). Từ đó suy ra \(\cos {{2\pi } \over 5} = {{ - 1 + \sqrt 5 } \over 4}\)

Giải chi tiết:

Với \(z \ne 0,\)

\({z^4} + {z^3} + {z^2} + z + 1 = {z^2}\left( {{z^2} + {1 \over {{z^2}}} + z + {1 \over z} + 1} \right)\)

\( = {z^2}\left( {{{\left( {z + {1 \over z}} \right)}^2} + \left( {z + {1 \over z}} \right) - 1} \right) \)

\(= {z^2}\left( {{{\rm{w}}^2} + {\rm{w}} - 1} \right)\), trong đó \({\rm{w}} = z + {1 \over z}\)

Phương trình \({{\rm{w}}^2} + {\rm{w}} - 1 = 0\) có hai nghiệm là \({{ - 1 \pm \sqrt 5 } \over 2}\)

Vì \({z_1},{z_2},{z_3},{z_4}\) là bốn nghiệm của phương trình \({z^4} + {z^3} + {z^2} + z + 1 = 0\) tức là nghiệm của phương trình:

\({\left( {z + {1 \over z}} \right)^2} + \left( {z + {1 \over z}} \right) - 1 = 0\) và \({z_4} = {\bar z_1} = {1 \over {{z_1}}},{z_3} = {\bar z_2} = {1 \over {{z_2}}}\) nên \({z_1} + {1 \over {{z_1}}},{z_2} + {1 \over {{z_2}}}\) là hai nghiệm phân biệt của phương trình \({{\rm{w}}^2} + {\rm{w}} - 1 = 0\)

Từ đó suy ra \(2\cos {{2\pi } \over 5} = {{ - 1 + \sqrt 5 } \over 2}\) (còn \(2\cos {{4\pi } \over 5} = {{ - 1 - \sqrt 5 } \over 2}\)) để ý rằng \(\cos {{2\pi } \over 5} > 0,\cos {{4\pi } \over 5} < 0\) (h.4.14)