Bài 3 trang 121 SGK Hình học 11

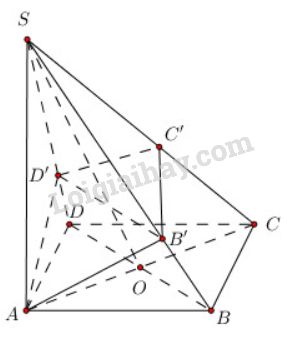
Đề bài

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh \(SA\) bằng \(a\) và vuông góc với mặt phẳng \((ABCD)\).

a) Chứng minh rằng bốn mặt bên của hình chóp là những tam giác vuông.

b) Mặt phẳng \((α)\) đi qua \(A\) và vuông góc với cạnh \(SC\) lần lượt cắt \(SB, SC\) và \(SD\) tại \(B’, C’\) và \(D’\). Chứng minh \(B’D’\) song song với \(BD\) và \(AB’\) vuông góc với \(SB\).

Lời giải chi tiết

a) \(SA \bot \left( {ABCD} \right) \) \(\Rightarrow SA \bot AB;\,\,SA \bot AD\)\( \Rightarrow \Delta SAB,\,\,\Delta SAD\) là các tam giác vuông tại \(A\).

Ta có:

\(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB \Rightarrow \Delta SBC\) vuông tại \(B\).

Tương tự:

\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot SD\)\( \Rightarrow \Delta SCD\) vuông tại \(D\).

b) Ta có \(BC \bot \left( {SAB} \right)\,\,\left( {cmt} \right) \Rightarrow AB' \bot BC.\)

\(\left\{ \begin{array}{l}
SC \bot \left( \alpha \right)\\
AB' \subset \left( \alpha \right)
\end{array} \right. \Rightarrow SC \bot AB'\)

\(\left\{ \begin{array}{l}
AB' \bot BC\\
AB' \bot SC
\end{array} \right. \Rightarrow AB' \bot \left( {SBC} \right)\)

\(\Rightarrow AB' \bot SB\).

Chứng minh tương tự ta có \(AD' \bot \left( {SCD} \right) \Rightarrow AD' \bot SD\).

Dễ thấy \(\Delta SAD = \Delta SAB\left( {c.g.c} \right)\) \( \Rightarrow AB' = AD'\) (hai đường cao cùng xuất phát từ một đỉnh)

\( \Rightarrow \Delta SAD' = \Delta SAB'\) \( \Rightarrow SD' = SB'\) (cạnh tương ứng)

Mà \(SD = SB\) (do \(\Delta SAD = \Delta SAB\)) nên \(\dfrac{{SD'}}{{SD}} = \dfrac{{SB'}}{{SB}} \Rightarrow B'D'//BD\)

Cách khác:

b) Ta có thể chứng minh \(B'D'//BD\) như sau:

\(\begin{array}{l}
SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BD\\
\left\{ \begin{array}{l}
BD \bot AC\\
BD \bot SA
\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\\
\Rightarrow BD \bot SC\\
SC \bot \left( {AB'C'D'} \right)\\
\Rightarrow BD//\left( {AB'C'D'} \right)\\
\left\{ \begin{array}{l}
BD//\left( {AB'C'D'} \right)\\
BD \subset \left( {SBD} \right)\\
\left( {SBD} \right) \cap \left( {AB'C'D'} \right) = B'D'
\end{array} \right.\\
\Rightarrow B'D'//BD
\end{array}\)

Loigiaihay.com