Bài 2.28 trang 34 SBT Đại số 10 Nâng cao

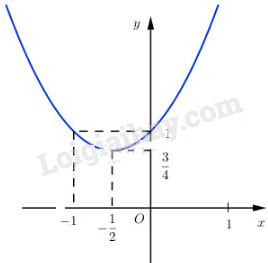
LG a

\(y = {x^2} + x + 1;\)

Lời giải chi tiết:

Ta có thể viết hàm số \(y = {x^2} + x + 1\) dưới dạng

\(y = {\left( {x + {1 \over 2}} \right)^2} + {3 \over 4}\)

Từ đó suy ra đồ thị của nó là một parabol hướng bề lõm lên trên và có đỉnh tại \(\left( { - {1 \over 2};{3 \over 4}} \right)\) ; hàm số đã cho nghịch biến trên khoảng \(\left( { - \infty ; - {1 \over 2}} \right)\) , đồng biến trên khoảng \(\left( { - {1 \over 2}; + \infty } \right)\)

và có giá trị nhỏ nhất bằng \({3 \over 4}\) khi \(x =  - {1 \over 2}.\)

Để vẽ đồ thị của hàm số này, ta lập bảng một vài giá trị của nó như sau

Đồ thị của hàm số có dạng như hình sau:

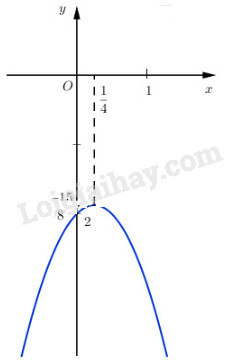
LG b

\(y =  - 2{x^2} + x - 2;\)

Lời giải chi tiết:

Đưa hàm số đã cho về dạng \(y =  - 2{\left( {x - {1 \over 4}} \right)^2} - {{15} \over 8}.\)

Từ đó suy ra hàm số đồng biến trên khoảng \(\left( { - \infty ;{1 \over 4}} \right)\) , nghịch biến trên khoảng \(\left( {{1 \over 4}; + \infty } \right)\) và có giá trị lớn nhất bằng \( - {{15} \over 8}\) khi \(x = {1 \over 4}.\).

Đồ thị hàm số:

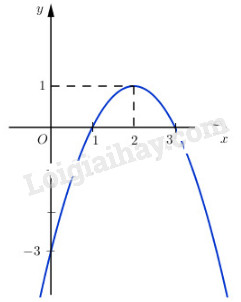
LG c

 \(y =  - {x^2} + 2x - 1;\)

Lời giải chi tiết:

Hàm số \(y =  - {x^2} + 2x - 1\) đồng biến trên khoảng \(\left( { - \infty ;2} \right)\); nghịch biến trên khoảng \(\left( {2; + \infty } \right)\).

Đồ thị hàm số:

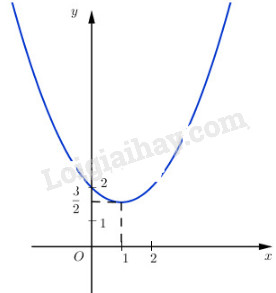
LG d

 \(y = {1 \over 2}{x^2} - x + 2.\)

Lời giải chi tiết:

 Hàm số \(y = {1 \over 2}{x^2} - x + 2.\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\); nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\)

Đồ thị hàm số:

Loigiaihay.com