Câu 21 trang 118 Sách bài tập Hình học 11 Nâng caoGiải bài tập Câu 21 trang 118 Sách bài tập Hình học 11 Nâng cao Quảng cáo
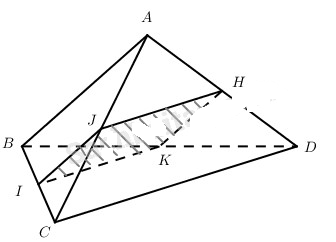
Đề bài Cho tứ diện ABCD. Gọi I, J, H, K lần lượt là trung điểm của BC, AC, AD, BD. Hãy tính góc giữa hai đường thẳng AB và CD trong các trường hợp sau: a) Tứ giác IJHK là hình thoi có đường chéo \(IH = \sqrt 3 IJ\). b) Tứ giác IJHK là hình chữ nhật Lời giải chi tiết Góc giữa hai đường thẳng AB và CD bằng góc giữa hai đường thẳng IJ và IK, đó là góc \(\widehat {JIK}\) hoặc \({180^0} - \widehat {JIK}\). a) Vì hình tứ giác IJHK là hình thoi mà \(IH = \sqrt 3 IJ\), nên từ \(I{K^2} + I{H^2} = 4I{J^2}\). ta có: \(I{K^2} = I{J^2}\) hay IK = IJ Như vậy JIK là tam giác đều, do đó \(\widehat {JIK} = {60^0}\). Vậy góc giữa AB và CD trong trường hợp này bằng 60°. b) Khi tứ giác IJHK là hình chữ nhật thì \(\widehat {JIK} = {90^0}\). Do đó, góc giữa AB và CD bằng 90°. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
