Câu 20 trang 118 Sách bài tập Hình học 11 Nâng cao

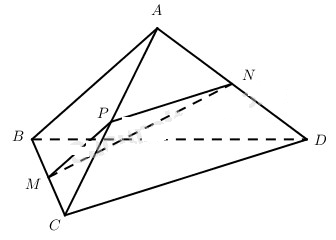
Đề bài

Cho tứ diện ABCD. Lấy các điểm M và N lần lượt thuộc các đường thẳng BC và AD sao cho \(\overrightarrow {MB}  = k\overrightarrow {MC} \) và \(\overrightarrow {NA}  = k\overrightarrow {ND} \) với k là số thực khác 0 cho trước. Đặt α là góc giữa hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {BA} \) ; β là góc giữa hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {C{\rm{D}}} \). Tìm mối liên hệ giữa AB và CD để \(\alpha  = \beta  = {45^0}\).

Lời giải chi tiết

Kẻ MP // AB thì dễ thấy NP // CD. Từ đó, góc giữa \(\overrightarrow {MN} \) và \(\overrightarrow {BA} \) bằng góc giữa ­\(\overrightarrow {MN} \) và \(\overrightarrow {MP} \), đó là góc \(\widehat {PMN}\). Góc giữa \(\overrightarrow {MN} \) và \(\overrightarrow {C{\rm{D}}} \) bằng góc giữa \(\overrightarrow {MN} \) và \(\overrightarrow {PN} \), đó là góc \(\widehat {PNM}\).

Vậy hai góc trên bằng nhau và bằng 45° khi và chỉ khi:

MP = NP và \(\widehat {MPN} = {90^0}\)

Từ đó, suy ra \({{CP} \over {CA}}.AB = {{AP} \over {AC}}.C{\rm{D}}\)  và \(AB \bot C{\rm{D}}\)

hay \({{AB} \over {C{\rm{D}}}} = {{AP} \over {CP}}\)  và \(AB \bot C{\rm{D}}\)

Mặt khác, ta có \(\overrightarrow {PA}  = k\overrightarrow {PC}  \Rightarrow {{AP} \over {PC}} = \left| k \right|\) .

Vậy giữa AB và CD có mối liên hệ

\({{AB} \over {C{\rm{D}}}} = \left| k \right|\)  và \(AB \bot C{\rm{D}}\)

thì góc giữa hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {BA} \) bằng góc giữa hai vectơ \(\overrightarrow {MN} \) và \(\overrightarrow {C{\rm{D}}} \), cùng bằng 45°).

Loigiaihay.com