Bài 1.59 trang 18 SBT Đại số và Giải tích 11 Nâng cao

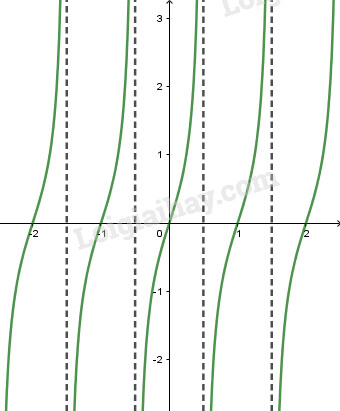
LG a

Tìm tập xác định của hàm số \(y = f(x)\);

Lời giải chi tiết:

Hàm số \(y = \tan (\pi x)\) xác định khi và chỉ khi \(\cos \left( {\pi x} \right) \ne 0.\)

Mặt khác

\(\cos \left( {\pi x} \right) = 0\)

\( \Leftrightarrow {\pi x}={\pi  \over 2} + k\pi \)

\(\Leftrightarrow x = {1 \over 2} + k\left( {k \in Z} \right)\)

Từ đó suy ra tập xác định của hàm số \(y = \tan (\pi x)\) là: \(D = R\backslash \left\{ {{1 \over 2} + k|k \in Z} \right\}\)

LG b

Chứng minh rằng với mọi số nguyên k , ta có \(f(x + k) = f(x)\) . Từ đó suy ra \(y = f(x)\) là hàm số tuần hoàn với chu kì T = 1;

Lời giải chi tiết:

Với mọi \(k \in Z,\) ta có

\(f\left( {x + k} \right) = \tan \left[ {\pi \left( {x + k} \right)} \right] \)

\(= \tan \left( {\pi x + k\pi } \right) \)

\(= \tan \left( {\pi x} \right) = f\left( x \right)\)

Trong các số nguyên dương, số 1 là nhỏ nhất.

Do đó \(\tan (\pi x)\) là hàm số tuần hoàn với chu kì \(T = 1\).

LG c

Cho biết sự biến thiên của hàm số \(y = f(x)\) trên mỗi khoảng \(\left( { - {1 \over 2} + k;{1 \over 2} + k} \right),k \in Z\);

Lời giải chi tiết:

Ta thấy

\( - {1 \over 2} + k < x < {1 \over 2} + k\)

\(\Leftrightarrow  - {\pi  \over 2} + k\pi  < \pi x < {\pi  \over 2} + k\pi \)

Từ đó suy ra hàm số \(\tan (\pi x)\) đồng biến trên mỗi khoảng \(\left( { - {1 \over 2} + k;{1 \over 2} + k} \right),\,k \in Z\)

LG d

Vẽ đồ thị của hàm số đó.

Lời giải chi tiết:

Đồ thị của hàm số có dạng như hình vẽ:

Loigiaihay.com