Bài 1.30 trang 16 SBT Giải tích 12 Nâng cao

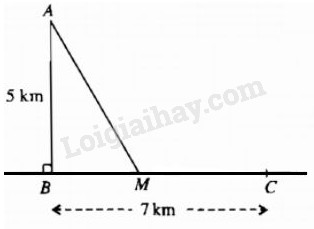
Đề bài

Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng AB = 5km. Trên bờ biền có một cái kho ở vị trí C cách B một khoảng là 7km. Người canh hải đăng có thể chèo đò từ A đến điểm M trên bờ biển với vận tốc 4 km/h rồi đi bộ đến C với vận tốc 6km/h (h.1.5).

Xác định vị trí của điểm M để người đó đến kho nhanh nhất.

Lời giải chi tiết

Đặt \(x = BM,0 \le x \le 7\).

Khi đó, \(AM = \sqrt {{x^2} + 25} ,MC = 7 - x.\) 

Thời gian người canh hải đăng đi từ A đến C là

\(T(x) = {{\sqrt {{x^2} + 25} } \over 4} + {{7 - x} \over 6}\) (giờ) \(0 \le x \le 7\)

Ta tìm \(x\in [0;7]\) để T đạt GTNN như sau:

\(\begin{array}{l}
T'\left( x \right) = \frac{1}{4}.\frac{x}{{\sqrt {{x^2} + 25} }} - \frac{1}{6}\\
T'\left( x \right) = 0 \Leftrightarrow \frac{1}{4}.\frac{x}{{\sqrt {{x^2} + 25} }} - \frac{1}{6} = 0\\
\Leftrightarrow \frac{1}{4}.\frac{x}{{\sqrt {{x^2} + 25} }} = \frac{1}{6}\\
\Leftrightarrow 3x = 2\sqrt {{x^2} + 25} \\
\Leftrightarrow 9{x^2} = 4{x^2} + 100\\
\Leftrightarrow {x^2} = 20 \Leftrightarrow \left[ \begin{array}{l}
x = 2\sqrt 5 \in \left[ {0;7} \right]\\
x = - 2\sqrt 5 \notin \left[ {0;7} \right]
\end{array} \right.
\end{array}\)

Hàm số T đạt giá trị nhỏ nhất tại điểm \(x = 2\sqrt 5  \approx 4,472(km)\)

Loigiaihay.com