Bài tập 4 trang 140 Tài liệu dạy – học Toán 8 tập 1

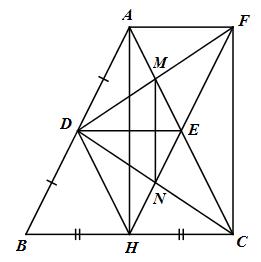
Đề bài

Cho tam giác ABC cân tại A. Gọi D, E, H lần lượt là trung điểm của AB, AC, BC.

a) Chứng minh rằng tứ giác ADHE là hình thoi.

b) Gọi F là điểm đối xứng của H qua E. CHứng minh rằng tứ giác AHCF là hình chữ nhật.

c) Gọi M là giao điểm của DF và AE; N là giao điểm của DC và HE. Chứng mih rằng DE là đường trung trực của MN.

Lời giải chi tiết

a) D, H lần lượt là trung điểm của AB và BC (gt)

\( \Rightarrow DH\) là đường trung bình của tam giác ABC \( \Rightarrow DH//AC\) và \(DH = {{AC} \over 2}\)

E, H lần lượt là trung điểm của AC và BC (gt)

\( \Rightarrow EH\) là đường trung bình của tam giác ABC \( \Rightarrow EH//AB\) và \(EH = {{AB} \over 2}\)

Ta có \(AD = DB = {{AB} \over 2}\) (D là trung điểm của AB)

\(AE = EC = {{AC} \over 2}\) (E là trung điểm của AC)

\(EH = {{AB} \over 2};\,EH = {{AC} \over 2};\,\,AB = AC\,\,(\Delta ABC\) cân tại A) \( \Rightarrow AD = DB = AE = EC = EH = DH\).

Tứ giác ADHE có \(AD = DH = HE = AE\) nên là hình thoi.

b) \(\Delta ABC\) cân tại A có AH là đường trung tuyến (H là trung điểm của BC)

\( \Rightarrow AH\) cũng là đường cao của tam giác ABC \( \Rightarrow AH \bot BC\) tại H.

Tứ giác AHCF có AC và HF cắt nhau tại E (gt)

E là trung điểm của AC (gt);

E là trung điểm của HF (F là điểm đối xứng của H qua E)

\( \Rightarrow \) Tứ giác AHCF là hình bình hành.

Mà \(\widehat {AHC} = {90^0}\,\,\left( {AH \bot BC} \right)\) nên AHCF là hình chữ nhật.

c) Tứ giác DECH có DH // EC (câu a) và \(DH = EC\,\,\left( { = {{AC} \over 2}} \right)\)

\( \Rightarrow DECH\) là hình bình hành.

Mà N là giao điểm của EH và DC, nên N là trung điểm của EH.

Tứ giác ADEF có \(AD = EF\,\,\left( { = EH} \right)\) và \(AD//EF\) \(\left( {AB//EH,\,\,D \in AB,\,\,E \in HF} \right)\)

Do đó tứ giác ADEF là hình bình hành

Mà M là giao điểm của AE và DF (gt) nên M là trung điểm của AE.

\(\Delta AEH\) có M, N lần lượt là trung điểm của AE và EH.

\( \Rightarrow MN\) là đường trung bình của tam giác AEH \( \Rightarrow MN//AH\)

Lại có \(AH \bot DE\) (ADHE là hình thoi) nên \(MN \bot DE\).

\(\Delta MEN\) có ED là đường cao \(\left( {MN \bot DE} \right)\), ED là đường phân giác (tứ giác ADHE là hình thoi) \( \Rightarrow \Delta MEN\) cân tại E.

Mà ED là đường cao \(\left( {ED \bot MN} \right)\) nên ED cũng là đường trung trực của MN.

Loigiaihay.com