Bài tập 3 trang 130 Tài liệu dạy – học Toán 7 tập 2 - Hình họcGiải bài tập Tam giác ABC vuông tại A (AB < AC). Vẽ đường cao AH. Trên tia đối của tia HC lấy điểm D sao cho HD = HC. Quảng cáo
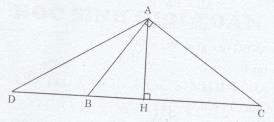
Đề bài Tam giác ABC vuông tại A (AB < AC). Vẽ đường cao AH. Trên tia đối của tia HC lấy điểm D sao cho HD = HC. a) Chứng minh rằng AC = AD. b) Chứng minh rằng \(\widehat {ADB} = \widehat {BAH}\) Lời giải chi tiết
a) Ta có:\(AH \bot CD\) tại H (gt) H là trung điểm của CD (HD = HC, \(H \in CD\)) => A thuộc đường trung trực của CD. Vậy AC = AD b) Ta có AC = AD => ∆ACD cân tại A \( \Rightarrow \widehat {ACD} = \widehat {ADB}\) (1) Mặt khác \(\widehat {BAH} + \widehat {ABH} = 90^\circ\) (∆ABH vuông tại H) \(\widehat {ACD} + \widehat {ABH} = 90^\circ\) (∆ABC vuông tại A) \( \Rightarrow \widehat {BAH} = \widehat {ACD}\) (2) Từ (1) và (2) \( \Rightarrow \widehat {ADB} = \widehat {BAH}\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
