Bài tập 20 trang 71 Tài liệu dạy – học Toán 8 tập 2

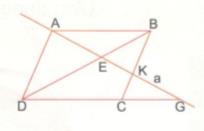
Đề bài

Cho hình bình hành ABCD. Đường thẳng a đi qua A lần lượt cắt BD, BC, DC theo thứ tự E, K, G. Chứng minh rằng:

\(\eqalign{  & a)\,\,A{E^2} = EK.EG  \cr  & b)\,\,{1 \over {AE}} = {1 \over {AK}} + {1 \over {AG}} \cr} \)

Lời giải chi tiết

a) Xét ∆DEG có \(DG//AB(DC//AB,G \in DC)\)

\( \Rightarrow {{AE} \over {EG}} = {{EB} \over {ED}}\) (hệ quả của định lý Thales) (1)

Xét ∆ADE có \(BK//AD(BC//AD,K \in BC)\)

\( \Rightarrow {{EB} \over {ED}} = {{EK} \over {AE}}\) (hệ quả của định lý Thales) (2)

Từ (1) và (2) suy ra \({{AE} \over {EG}} = {{EK} \over {AE}} \Rightarrow A{E^2} = EK.EG\)

b) Ta có \(EK.EG = A{E^2}\) (câu a) \( \Rightarrow {{EK} \over {AE}} = {{AE} \over {EG}} \Rightarrow {{EK} \over {AE}} = {{EK + AE} \over {AE + EG}} = {{AK} \over {AG}}\)

Ta có \({{EK} \over {AE}} = {{AK} \over {AG}} \Rightarrow {{AK - AE} \over {AE}} = {{AK} \over {AG}} \)

\(\Rightarrow {{AK} \over {AE}} - 1 = {{AK} \over {AG}}\)

\(\Rightarrow {{AK} \over {AE}} - {{AK} \over {AK}}= {{AK} \over {AG}}\)

\(\Rightarrow {1 \over {AE}} - {1 \over {AK}} = {1 \over {AG}}\)

Vậy \({1 \over {AE}} = {1 \over {AK}} + {1 \over {AG}}\)

Loigiaihay.com